2.4: Sequential Games

# 2.4: Sequential Games
## ECON 326 · Industrial Organization · Spring 2020
### Ryan Safner Assistant Professor of Economics <a href="mailto:safner@hood.edu"> safner@hood.edu</a> <a href="https://github.com/ryansafner/IOs20"> ryansafner/IOs20</a> <a href="https://IOs20.classes.ryansafner.com"> IOs20.classes.ryansafner.com</a>

---

# Wrapup of Oligopoly

1. .hi[Bertrand competition]
  - Firms **simultaneously** compete on **price**
2. .hi[Cournot competition]
  - Firms **simultaneously** compete on **quantity**
3. .hi[Stackelberg competition]
  - Firms **sequentially** compete on **quantity**

]

.pull-right[
.center[
![:scale 100%](https://www.dropbox.com/s/tymdsxbqaq2scxq/chessknights.jpg?raw=1)
]
]

---

# Wrapup of Oligopoly

- Output: `\(Q_m < Q_c < Q_s < Q_b\)`
- Market price: `\(P_b < P_s < P_c < P_m\)`
- Profit: `\(\pi_b=0 < \pi_s < \pi_c < \pi_m\)`

Where subscript `\(m\)` is monopoly (collusion), `\(c\)` is Cournot, `\(s\)` is Stackelberg, `\(b\)` is Bertrand

---

# Wrapup of Oligopoly

.center[
![:scale 50%](https://ios20.classes.ryansafner.com/slides/2.3-slides_files/figure-html/unnamed-chunk-6-1.png)
]

---

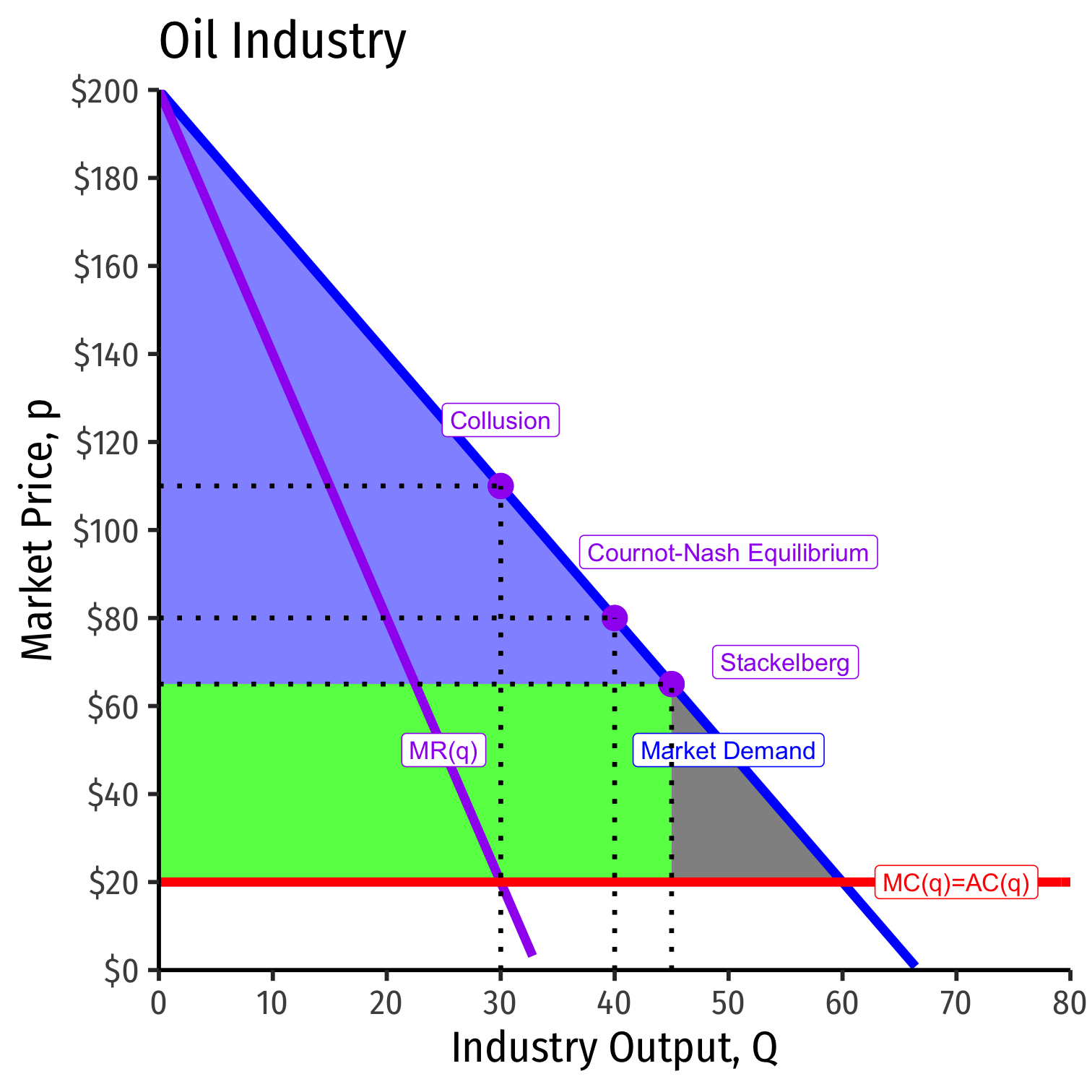
# Wrapup of Oligopoly

- See some visualizations I made:
  1. [Cournot: Symmetric Market Changes](https://ryansafner.shinyapps.io/Cournot_market_changes/)
  2. [Cournot: Asymmetric Costs](https://ryansafner.shinyapps.io/cournot_asymmetric_costs/)
  3. [Cournot: With n Firms](https://ryansafner.shinyapps.io/Cournot_n_firms/)

Major implications from Cournot:

1. As `\(\uparrow\)` number of firms: `\(\downarrow q\)`, `\(\downarrow p\)`, `\(\downarrow \pi\)`, `\(\uparrow CS\)`, `\(\downarrow DWL\)` (closer to perfect competition)

2. If a firm has lower costs than others, earns greater profit. Firms will want to (equivalently):
  - lower their own costs
  - raise rivals' costs

---

# Recall: Structure-Conduct-Performance Paradigm

- An industry's .hi-purple["Performance"]
  - Price (high, low)
  - Output (high, low)
  - Profit
  - Productive efficiency
  - Allocative efficiency (CS, DWL)
  - Quality, safety, etc.
]
---

# Recall: Structure-Conduct-Performance Paradigm

- ... which is determined by its firms' .hi-purple["Conduct"]
  - Pricing behavior
  - Output choices
  - Legal tactics
  - Entry and exit
  - Collusion
  - Competition
  - Innovation
]

---

# Recall: Structure-Conduct-Performance Paradigm

- ... which is determined by the industry's .hi-purple["Structure"]
  - Number of buyers
  - Number of sellers
  - Product differentiation
  - Vertical integration
  - Barriers to entry
]

---

# Recall: Structure-Conduct-Performance Paradigm

- ... which is determined by the product's .hi-purple["Technology"]
  - **Consumer demand** (price and income elasticity, substitutes, location, etc)
  - **Good's features**: inputs, technology, durability, rivalry, excludability
  - **Production features**: economies of scale, economies of scope, network externalities, two-sided platforms
]

---

# Recall: Structure-Conduct-Performance Paradigm

- .hi-purple[Government policy] can affect nearly every stage
  - Entry regulation
  - Price regulation
  - Antitrust regulation
  - Taxes and subsidies
]

---

# Game Theory: Generalizations

---

# Game Theory: Generalizations

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/tymdsxbqaq2scxq/chessknights.jpg?raw=1)
]
]

- As explore other aspects of firm behavior, we need more tools from game theory beyond a one-shot prisoners' dilemma

- We've seen examples of .hi-purple[continuous strategies] in Cournot, Bertrand, & Stackelberg competition
  - Firms can choose a wide range of prices, outputs
  - One-shot prisoners' dilemma we had two .hi-purple[discrete] choices

]

---

# Game Theory: Generalizations

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/tymdsxbqaq2scxq/chessknights.jpg?raw=1)
]
]

- Seen .hi-purple[simultaneous] (prisoners' dilemma) vs. .hi-purple[sequential] game (Stackelberg)

- Assumed .hi-purple[common knowledge] about the game structure. Everyone knows all players, all their potential strategies, and all of their payoffs

- .hi[Perfect information] (players can observe moves of others, as in sequential game) vs. .hi[Imperfect information] players cannot observe moves of others (Prisoners' Dilemma)
]

---

# Solution Concepts

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/j7xenkgo3p71vke/equilibriumbalance.png?raw=1)
]
]

- We use .hi-purple["solution concepts"] to allow us to predict an .hi-purple[equilibrium] of a game

- .hi[Nash Equilibrium] is the primarly solution concept
  - Note it has many variants depending on if games are sequential vs. simultaneous, perfect vs. imperfect information, etc.

]

---

# Solution Concepts: Nash Equilibrium

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/j7xenkgo3p71vke/equilibriumbalance.png?raw=1)
]
]

- Recall, .hi[Nash Equilibrium]: no players want to change their strategy given what everyone else is playing
  - All players are playing a best response to each other

]

---

# Solution Concepts: Nash Equilibrium

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/j7xenkgo3p71vke/equilibriumbalance.png?raw=1)
]
]

- Important about N.E.:
  - N.E. `\(\neq\)` the "best" pr optimal outcome
    - Recall the Prisoners' Dilemma!
  - Game may have **multiple** N.E.
  - Game may have **no** N.E. (in "pure" strategies)

]

---

# Sequential Games: Extensive Form

]

- We consider an .hi[Entry Game], a .hi-purple[sequential] game played between a potential .hi-red[Entrant] and an .hi-blue[Incumbent]

- A sequence of play: .hi-red[Entrant] moves first, .hi-blue[Incumbent] moves second

- Note: the magnitude of the payoffs don't really matter, only their **relative sizes**
  - Hence, my simple numbers
]

---

# Pure Strategies

.pull-left[
.center[
![](https://www.dropbox.com/s/564ocw8l263kngm/entry_game_extensive.png?raw=1)
]
]

- This game is depicted in .hi-purple["Extensive form"] or a .hi-purple[game tree]

- Each player faces at least one .hi-purple["decision node"] (solid, colored by player)
  - .hi-red[Entrant] chooses between .red[Enter] or .red[Stay Out] at node .red[E.1]
  - .hi-blue[Incumbent] chooses between .blue[Accommodate] or .blue[Fight] at .blue[I.1]
  - Game ends at any .hi-purple["terminal node"] (hollow node), and each player earns payoffs (.red[Entrant], .blue[Incumbent])

]

---

# Pure Strategies

.pull-left[
.center[
![](https://www.dropbox.com/s/564ocw8l263kngm/entry_game_extensive.png?raw=1)
]
]

- We need to talk more about .hi[strategies]

- .hi[Pure strategy]: a player's *complete* plan of action for every possible contingency
  - i.e. what a player will choose at *every* possible decision node
  - think like an algorithm:
  
> if we reach node 1, I will play X; if we reach node 2, I will play Y; if ...

- .hi-purple["Mixed strategy"]: play a strategy with some probability
]

---

# Solving a Sequential Game

.pull-left[
.center[
![](https://www.dropbox.com/s/564ocw8l263kngm/entry_game_extensive.png?raw=1)
]
]

- .hi-red[Entrant] has 2 pure strategies:
  1. .red[Stay Out] at .red[E.1]
  2. .red[Enter] at .red[E.1]

- .hi-blue[Incumbent] has 2 pure strategies:
  1. .blue[Accommodate] at .blue[I.1]
  2. .blue[Fight] at .blue[I.1]

- Note .hi-blue[Incumbent]'s strategy only comes into play if .hi-red[Entrant] plays .hi-red[Enter] and the game reaches node .hi-blue[I.1]

]

---

# Solving a Sequential Game

.pull-left[
.center[
![](https://www.dropbox.com/s/564ocw8l263kngm/entry_game_extensive.png?raw=1)
]
]

- .hi[Backwards induction]: to determine the outcome of the game, start with the **last-mover** (i.e. decision nodes just before terminal nodes)

- What is that mover's best choice to maximize their payoff?

- i.e. we start at .blue[I.1] where .hi-blue[Incumbent] can:
  - .blue[Accommodate] to earn .blue[1]
  - .blue[Fight] to earn .blue[0]

]

---

# Solving a Sequential Game

.pull-left[
.center[
![](https://www.dropbox.com/s/hpoouciwsg02d70/entry_game_extensive_last.png?raw=1)
]
]

- .hi-blue[Incumbent] will .hi-blue[Accommodate] if game reaches .hi-blue[I.1]

- Given this, what will .hi-red[Entrant] do at .hi-red[E.1]?
  - .red[Stay Out] to earn .red[1]
  - .red[Enter], knowing .hi-blue[Incumbent] will .blue[Accommodate], and so will earn .red[2]
]

---

# Solving a Sequential Game

.pull-left[
.center[
![](https://www.dropbox.com/s/w4dgdgmh9ptp80c/entry_game_extensive_rollback.png?raw=1)
]
]

- .hi-red[Entrant] will .red[Enter]

- Continue until we've reached the initial node (beginning)

- We have the outcome:

.center[
(.hi-red[Enter], .hi-blue[Accommodate])
]
- Some textbooks call this a .hi-purple["rollback equilibrium"]
]

---

# Sequential Games: Normal vs. Extensive Form

- Any game in extensive form can also be depicted in .hi-purple["normal"] or .hi-purple["strategic" form] (a payoff matrix)

- Note, if .hi-red[Entrant] plays .hi-red[Stay Out], doesn't matter what .hi-blue[Incumbent] plays, payoffs are the same

]

---

# Sequential Games: Normal vs. Extensive Form

- Solve this for Nash Equilibrium...

]

---

# Sequential Games: Normal vs. Extensive Form

- Solve this for Nash Equilibrium...

- There's no dominant strategies!

- Here's two methods that will help:

**1 -** .hi-purple[Cell-by-Cell Inspection]: look in each cell, does either player want to deviate?
  - .hi-purple[If No: a Nash Equilibrium]
  - If Yes: *not* a Nash Equilibrium

]

---

# Sequential Games: Normal vs. Extensive Form

**2 -** .hi-purple[Best-Response Analysis]: take the perspective of each player. If the *other* player plays a particular strategy, what is *your* strategy(s) that gets you the highest payoff?
  - Ties are allowed
  - .hi-purple[Any cell where *both* players are playing a best response is a Nash Equilibrium]
]

---

# Nash Equilibria

.pull-left[
.center[
![](https://www.dropbox.com/s/09ch2slydlrml7b/entry_game_normal_BR.png?raw=1)
]
]

- *Two* Nash Equilibria:
1. (.hi-red[Enter], .hi-blue[Accommodate])
2. (.hi-red[Stay Out], .hi-blue[Fight])

- But remember, we ignored the *sequential* nature of this game in normal form
  - Which Nash equilibrium is "sequentially rational?"

- New solution concept: .hi["subgame perfect Nash equilibrium" (SPNE)]
]

---

# Subgame Perfection

---

# Subgames

.pull-left[
.center[
![](https://www.dropbox.com/s/564ocw8l263kngm/entry_game_extensive.png?raw=1)
]
]

- .hi-purple[Subgame]: any portion of a full game beginning at one node and continuing until all terminal nodes
  - i.e. any decision node starts a subgame containing all the "branches" of that decision node

- Every full game is itself a subgame

- How many subgames does *this* game have?
]

---

# Subgames

.pull-left[
.center[
![](https://www.dropbox.com/s/p4zearozh64c055/entry_game_subgames.png?raw=1)
]
]

1. Subgame initiated at decision node .hi-red[E.1] (i.e. the full game)
2. Subgame initiated at decision node .hi-blue[I.1]

]

---

# Subgame Perfect Nash Equilibrium

.pull-left[
.center[
![](https://www.dropbox.com/s/p4zearozh64c055/entry_game_subgames.png?raw=1)
]
]

- Consider each subgame as a game itself and ignore the .hi-purple["history"] of play that got a to that subgame
  - What is optimal to play in *that* subgame?

- Consider a set of strategies that is optimal for all players in *every* subgame it reaches

- That is a .hi["subgame perfect Nash equilibrium"]

]

---

# Subgame Perfect Nash Equilibrium

.pull-left[
.center[
![:scale 75%](https://www.dropbox.com/s/p4zearozh64c055/entry_game_subgames.png?raw=1)

![:scale 80%](https://www.dropbox.com/s/09ch2slydlrml7b/entry_game_normal_BR.png?raw=1)

]
]

- Recall our two Nash Equilibria from normal form: 
1. (.hi-red[Enter], .hi-blue[Accommodate])
2. (.hi-red[Stay Out], .hi-blue[Fight])

]

---

# Subgame Perfect Nash Equilibrium

.pull-left[
.center[
![:scale 75%](https://www.dropbox.com/s/p4zearozh64c055/entry_game_subgames.png?raw=1)

![:scale 80%](https://www.dropbox.com/s/09ch2slydlrml7b/entry_game_normal_BR.png?raw=1)

]
]

- Recall our two Nash Equilibria from normal form: 
1. (.hi-red[Enter], .hi-blue[Accommodate])
2. (.hi-red[Stay Out], .hi-blue[Fight])

- Consider the second set of strategies, where .hi-blue[Incumbent] chooses to .blue[Fight] at node .blue[I.1]

- What if for some reason, .hi-blue[Incumbent] is playing this strategy, and .hi-red[Entrant] unexpectedly plays .red[Enter]??
]

---

# Subgame Perfect Nash Equilibrium

.pull-left[
.center[
![:scale 75%](https://www.dropbox.com/s/p4zearozh64c055/entry_game_subgames.png?raw=1)

![:scale 80%](https://www.dropbox.com/s/09ch2slydlrml7b/entry_game_normal_BR.png?raw=1)

]
]

- It's **not rational** for .hi-blue[Incumbent] to play .blue[Fight] if the game reaches .blue[I.1]!
  - Would want to switch to .blue[Accommodate]!

- .hi-blue[Incumbent] playing .hi-blue[Fight] at .blue[I.1] is **not a Nash Equilibrium in this subgame!**

- Thus, Nash Equilibrium (.hi-red[Stay Out], .hi-blue[Fight]) is **not sequentially rational**
  - It *is* still a Nash equilibrium!
]

---

# Subgame Perfect Nash Equilibrium

.pull-left[
.center[
![:scale 75%](https://www.dropbox.com/s/6kl6h8nmi1t39hy/entry_game_rollback_subgames.png?raw=1)

![:scale 80%](https://www.dropbox.com/s/09ch2slydlrml7b/entry_game_normal_BR.png?raw=1)

]
]

- Only (.hi-red[Enter], .hi-blue[Accommodate]) is a .hi-purple[Subgame Perfect Nash Equilibrium (SPNE)]

- These strategy profiles for each player constitute a Nash equilibrium in every possible subgame!

- Simple connection: "rollback equilibrium" is always SPNE!
]

---

# SPNE and Credibility

.pull-left[
.center[
![:scale 75%](https://www.dropbox.com/s/6kl6h8nmi1t39hy/entry_game_rollback_subgames.png?raw=1)

![:scale 80%](https://www.dropbox.com/s/09ch2slydlrml7b/entry_game_normal_BR.png?raw=1)

]
]

- Suppose before the game started, .hi-blue[Incumbent] announced to .hi-red[Entrant], "if you .red[Enter], I will .blue[Fight]!"

- This **threat** is .hi-purple[not credible] because playing .blue[Fight] in response to .red[Enter] is not rational!

- The strategy is not Subgame Perfect!

]

---

# SPNE and Credibility

- Suppose I were to announce that if you were late once to class, I gave you an F

- If you believe my threat, you would arrive on time, and I never have to carry out my threat

- Sounds like a Nash equilibrium...but not subgame perfect!

- If you call my bluff and come late, I don't actually want to carry out my policy!
]

---

# Incentive Compatibility

![:scale 80%](https://www.dropbox.com/s/9ehcegb01kbhk28/bluff.jpeg?raw=1)
]
]

- .hi-purple["Talk is cheap"]

- With perfect information, **promises** or **threats** will not change equilibrium if they are .hi-purple[not credible]
  - Must be "sequentially rational" or SPNE strategy

- Strategy must be .hi-purple[incentive-compatible], if game reaches the relevant node, it must be in your interest to carry out your promise or threat!
]

---

# Credible Commitment

![:scale 80%](https://www.dropbox.com/s/9ehcegb01kbhk28/bluff.jpeg?raw=1)
]
]

- Threats and promises can be .hi-purple[credible] with .hi[commitment]

- A .hi[commitment] changes the game in a way that forces you to carry out your promise or threat
  - tying your own hands makes you stronger!
]

---

# Credible Commitment

*Odysseus and the Sirens* by John William Waterhouse, Scene from Homer's *The Odyssey*

]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![:scale 65%](https://www.dropbox.com/s/hfzmi9modl88nfn/cableconstruction.jpg?raw=1)

![:scale 65%](https://www.dropbox.com/s/z3q98vngkautezz/cableinfrastructure.jpg?raw=1)

]
]

- Suppose that before .hi-red[Entrant] can decide to .red[Enter] or .red[Stay Out], .hi-blue[Incumbent] can choose to .blue[Invest] in excess capacity

- i.e. builds up a "war chest" of superfluous infrastructure that costs .blue[-1]

- But with it, in response to .hi-red[Entrant] playing .red[Enter], .hi-blue[Incumbent] is in a better position to .blue[Fight] a price war that kicks .hi-red[Entrant] out of the market
]

---

# Entry Game with Credible Commitment

]
]

.pull-right[
- Game changes, .hi-blue[Incumbent] goes first at (new) .blue[I.1], deciding whether to .blue[Invest] or .blue[Don't]
  - Game is the same as before from .red[E.2] onwards
  
- This is a more complicated game, let's apply what we've learned...
]

---

]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/o6b1825xy53m5rt/entry_game_commitment.png?raw=1)

]
]

]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/ha8466nx5g4ind3/entry_game_commitment_subgames.png?raw=1)

]
]

1. Subgame initiated by node .blue[I.1] (game itself)
2. Subgame initiated by node .red[E.1] 
3. Subgame initiated by node .red[E.2]
4. Subgame initiated by node .blue[I.2] 
5. Subgame initiated by node .blue[I.3]

]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/o6b1825xy53m5rt/entry_game_commitment.png?raw=1)

]
]

- What are the **strategies** available to each player?

]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/o6b1825xy53m5rt/entry_game_commitment.png?raw=1)

]
]

- What are the **strategies** available to each player?

- .hi-red[Entrant], choosing at nodes .red[(E.1, E.2)]
  1. .red[(Stay Out, Stay Out)]
  2. .red[(Stay Out, Enter)]
  3. .red[(Enter, Stay Out)]
  4. .red[(Enter, Enter)]

]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/o6b1825xy53m5rt/entry_game_commitment.png?raw=1)

]
]

- What are the **strategies** available to each player?

- .hi-blue[Incumbent], choosing at nodes .blue[(I.1, I.2, I.3)]
  1. .blue[(Invest, Accommodate, Accommodate)]
  2. .blue[(Invest, Accommodate, Fight)]
  3. .blue[(Invest, Fight, Accommodate)]
  4. .blue[(Invest, Fight, Fight)]
  5. .blue[(Don't, Accommodate, Accommodate)]
  6. .blue[(Don't, Accommodate, Fight)]
  7. .blue[(Don't, Fight, Accommodate)]
  8. .blue[(Don't, Fight, Fight)]

]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![:scale 100%](https://www.dropbox.com/s/o6b1825xy53m5rt/entry_game_commitment.png?raw=1)

]

- We can use backwards induction to find the outcome of the game

- Start with best response of .hi-blue[Incumbent] at .blue[I.2] and .blue[I.3]...then best response of .hi-blue[Entrant] at .red[E.1] and .red[E.2]...then .hi-blue[Incumbent] at .blue[I.1]
]

---

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![](https://www.dropbox.com/s/wxvnuilir0396ue/entry_game_commitment_rollback.png?raw=1)
]

]

- Define the outcome in terms of their strategies:

`\(\big \{\)` .blue[(Invest, Fight, Accommodate)], .red[(Stay Out, Enter)] `\(\big \}\)`

- The **equilibrium path of play** is .blue[Invest], then .red[Stay Out]

- Note via backward induction, we've shown the optimal response by each player at each decision node
]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![](https://www.dropbox.com/s/0569yfpt0llmmtc/entry_game_commitment_SPNE.png?raw=1)
]

]

`\(\big \{\)` .blue[(Invest, Fight, Accommodate)], .red[(Stay Out, Enter)] `\(\big \}\)`

- SPNE: this set of strategies induces a Nash equilibrium in every subgame
  - Each player optimally responding to every contigency

- With **commitment**, it is .hi-purple[credible] for .blue[Incumbent] to threaten to .blue[Fight] if .red[Entrant] decides to .red[Enter]!
]

---

# Entry Game with Credible Commitment

.pull-left[
.center[
![](https://www.dropbox.com/s/p4bfrosh8obt1ht/entry_game_commitment_normal_SPNE.png?raw=1)
]

]

`\(\big \{\)` .blue[(Invest, Fight, Accommodate)], .red[(Stay Out, Enter)] `\(\big \}\)`

- Note we could look at the set of strategies in normal form

- Using best response, there are *many* Nash Equilibria (boldened)!
  - But only the one we mentioned is subgame perfect!

]