+ - 0:00:00
Notes for current slide
Notes for next slide

1.2: Technology and Cost

ECON 326 · Industrial Organization · Spring 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/IOs20
IOs20.classes.ryansafner.com

Models Refresher

The Two Major Models of Price Theory

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

The Two Major Models of Price Theory

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

Equilibrium

  • Agents compete with others over scarce resources

  • Agents adjust behaviors based on prices

  • Stable outcomes when adjustments stop

Relationship Between Optimization & Equilibrium

  • If people can learn and change their behavior, they will always switch to a higher-valued option

  • If there are no alternatives that are better, people are at an optimum

  • If everyone is at an optimum, the system is in equilibrium

Constrained Optimization III

  • All constrained optimization models have three moving parts:
  1. Choose: < some alternative >

Constrained Optimization III

  • All constrained optimization models have three moving parts:

  1. Choose: < some alternative >

  2. In order to maximize: < some objective >

Constrained Optimization III

  • All constrained optimization models have three moving parts:

  1. Choose: < some alternative >

  2. In order to maximize: < some objective >

  3. Subject to: < some constraints >

This Black Box We Call "Firms"

  • Firm is a mere production process:

    • a bundle of technology, physical assets, and individuals

  • Synonymous with production function

  • Fully replicable

  • We'll explore (and explode) this much later

What Do Firms Do? I

  • Assume "firm" is agent to model:

  • So what do firms do?

  • How would we set up an optimization model:

  1. Choose: < some alternative >

  2. In order to maximize: < some objective >

  3. Subject to: < some constraints >

What Do Firms Do? II

  • Firms convert some goods to other goods:

What Do Firms Do? II

  • Firms convert some goods to other goods:

  • Inputs: x1,x2,⋯,xn

    • Examples: worker efforts, warehouse space, electricity, loans, gasoline, cardboard, fertilizer, computers, software programs, etc

What Do Firms Do? II

  • Firms convert some goods to other goods:

  • Inputs: x1,x2,⋯,xn

    • Examples: worker efforts, warehouse space, electricity, loans, oil, fertilizer, software programs, etc

  • Output: q

    • Examples: gasoline, cars, legal services, mobile apps, vegetables, consulting advice, financial reports, etc

What Do Firms Do? III

  • Technology or a production function: rate at which firm can convert specified inputs (x1,x2,⋯,xn) into output (q) q=f(x1,x2,⋯,xn)

Production Function as Recipe

The production function

The production algorithm

Factors of Production I

q=f(t,l,k,e,a)

  • Economists typically classify inputs in categories, known as the factors of production (FOP) or "the factors"
Factor Owned By Earns
Land (t) Landowners Rent
Labor (l) Laborers Wages
Capital (k) Capitalists Interest
Entrepreneurship (e) Entrepreneurs Profit
  • a: "total factor productivity" (ideas/knowledge/institutions)

Factors of Production II

q=f(l,k)

  • We will assume just two inputs: labor l and capital k
Factor Owned By Earns
Labor (l) Laborers Wages
Capital (k) Capitalists Interest

What Does a Firm Maximize?

  • We will assume firms maximize profit (π)

  • Not true for all firms

    • Examples: non-profits, charities, civic associations, government agencies, criminal organizations, etc

  • Even profit-seeking firms may also want to maximize additional things

    • Examples: goodwill, sustainability, social responsibility, etc

What is Profit?

  • In economics, profit is simply benefits minus (opportunity) costs

What is Profit?

  • In economics, profit is simply benefits minus (opportunity) costs

  • Suppose a firm sells output q at a price p

What is Profit?

  • In economics, profit is simply benefits minus (opportunity) costs

  • Suppose a firm sells output q at a price p

  • It can buy each input xi at an associated price pi
    • labor l at wage rate w
    • capital k at rental rate r

What is Profit?

  • In economics, profit is simply benefits minus (opportunity) costs

  • Suppose a firm sells output q at a price p

  • It can buy each input xi at an associated price pi

    • labor l at wage rate w
    • capital k at rental rate r

  • The profit of selling q units and using inputs l,k is: π=pq⏟revenues−(wl+rk)⏟costs

Who Gets the Profits? I

π=pq⏟revenues−(wl+rk)⏟costs

  • The firm's costs are all of the factor-owner's incomes!

    • Landowners, laborers, creditors are all paid rent, wages, and interest

  • Profits are the residual value leftover after paying all factors

Who Gets the Profits? II

π=pq⏟revenues−(wl+rk)⏟costs

  • Profits are income for the residual claimant(s) of the production process (i.e. owner(s) of a firm):
    • Entrepreneurs
    • Shareholders

Who Gets the Profits? III

π=pq⏟revenues−(wl+rk)⏟costs

  • Residual claimants have incentives to maximize firm's profits, as this maximizes their own income

  • Entrepreneurs and shareholders are the only participants in production that are not guaranteed an income!

    • Starting and owning a firm is inherently risky!

The Firm's Optimization Problem I

  • So what do firms do?

  1. Choose: < some alternative >

  2. In order to maximize: < profits >

  3. Subject to: < technology >

  • We've so far assumed they maximize profits and they are limited by their technology

The Firm's Optimization Problem II

  • What do firms choose? (Not an easy answer)

  • Prices?

    • Depends on the market the firm is operating in!
    • Study of industrial organization

  • Essential question: how competitive is a market? This will influence what firms (can) do

The "Runs" of Production

  • The "time"-frame of production can be usefully divided between short vs. long run analysis

  • Short run: at least one factor of production is fixed* (too costly to change) q=f(ˉk,l)

    • We assume capital is fixed (i.e. number of factories, storefronts, etc)
    • Only decisions about how to use labor

The "Runs" of Production

  • The "time"-frame of production can be usefully divided between short vs. long run analysis

  • Long run: all factors of production are variable q=f(k,l)

Marginal Products

  • Marginal product of an input is the additional output produced by one more unit of that input (holding other inputs constant)

  • Like marginal utility

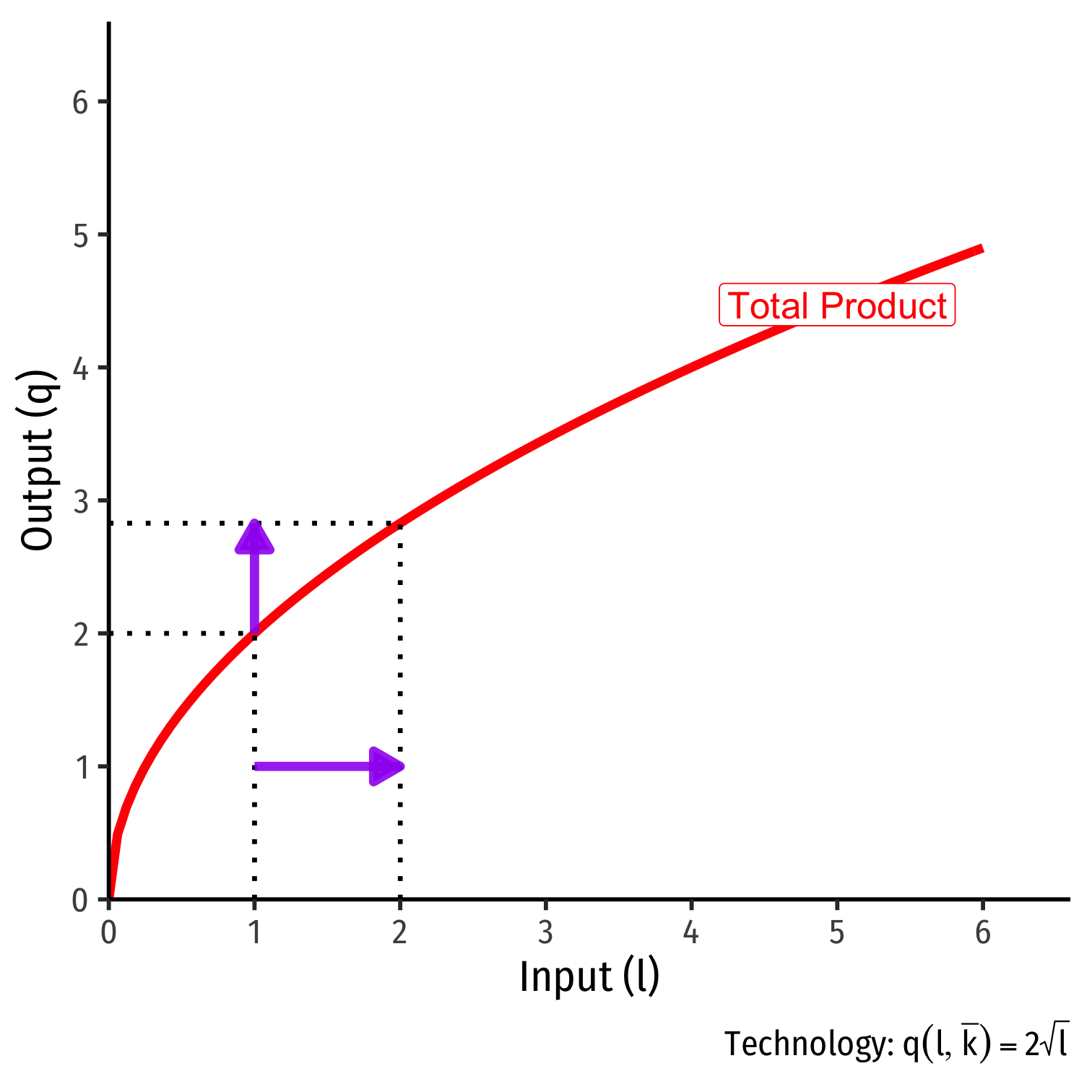
Marginal Product of Labor

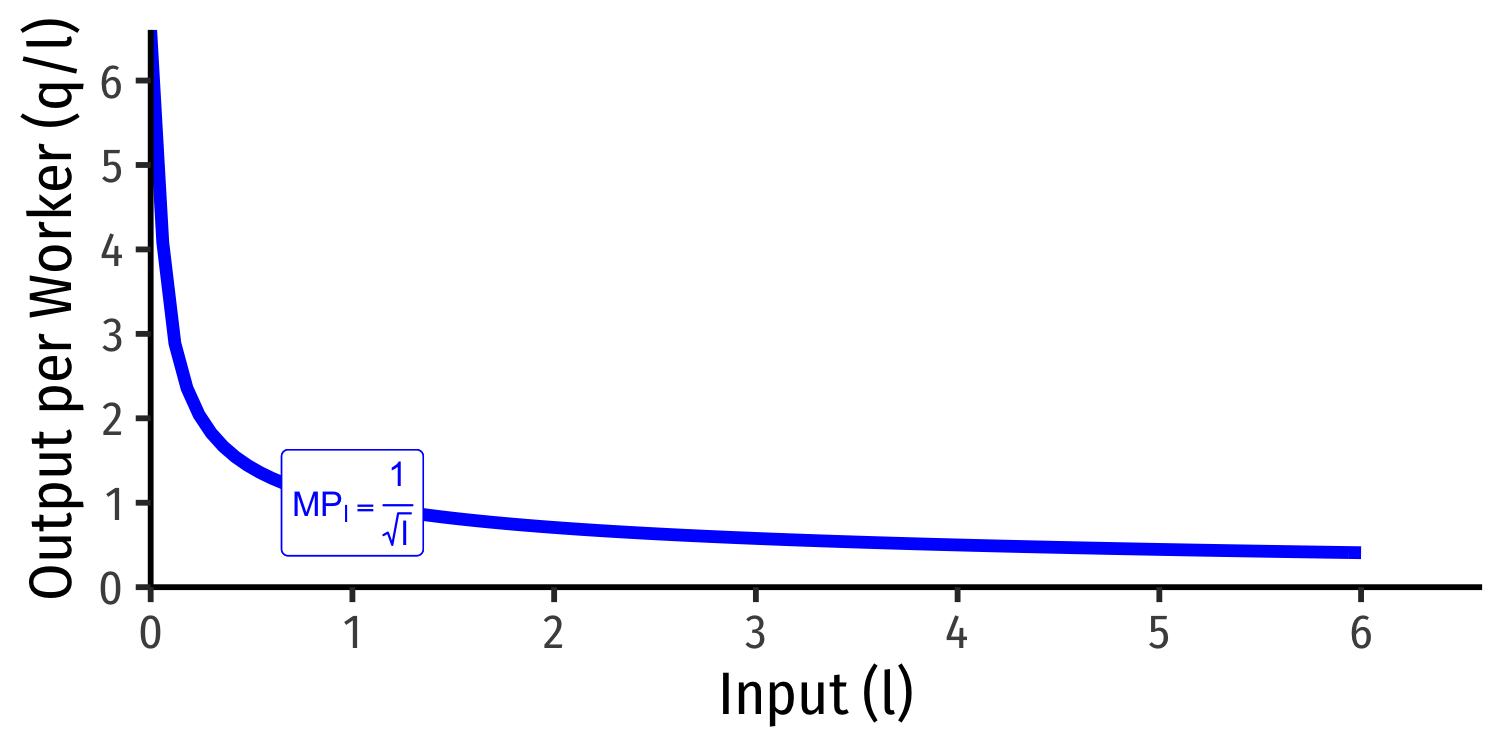
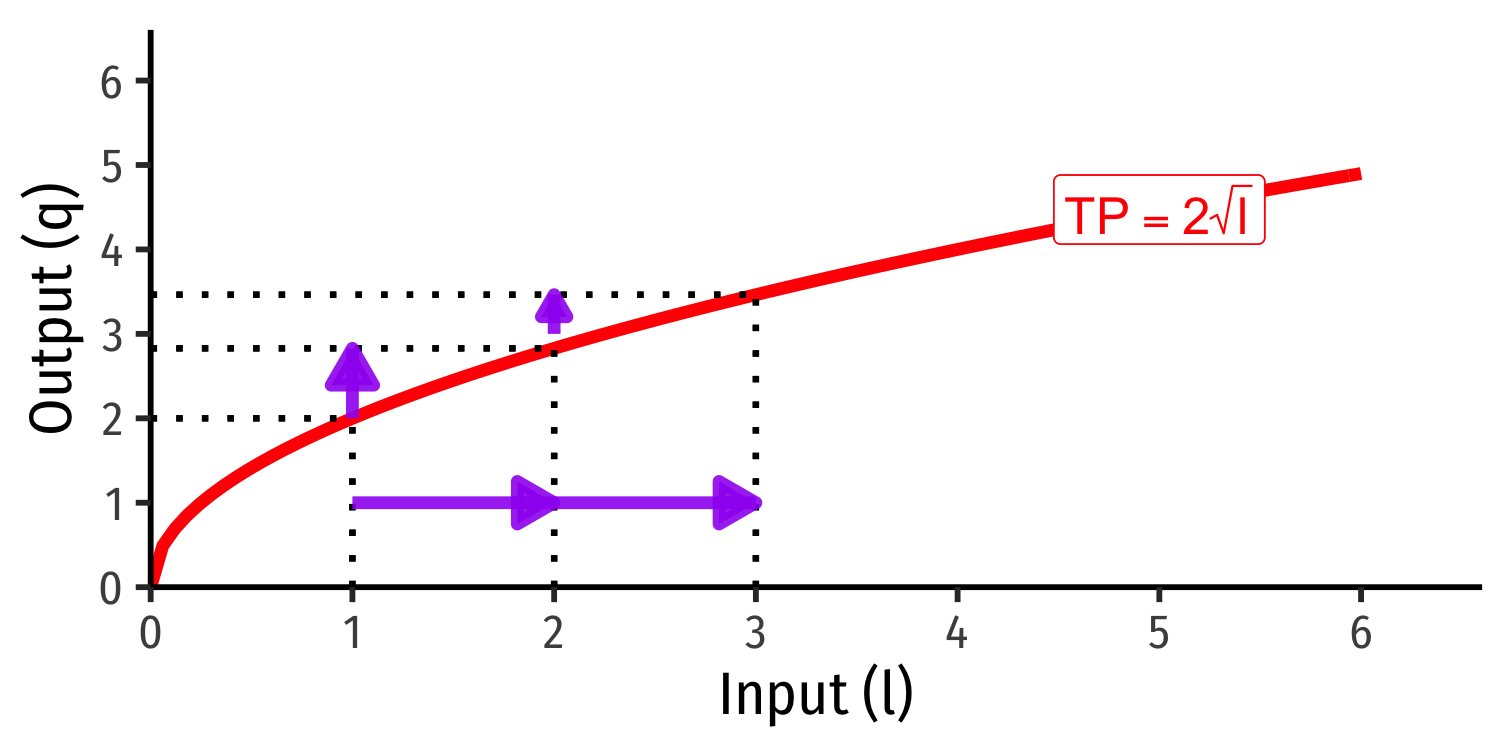
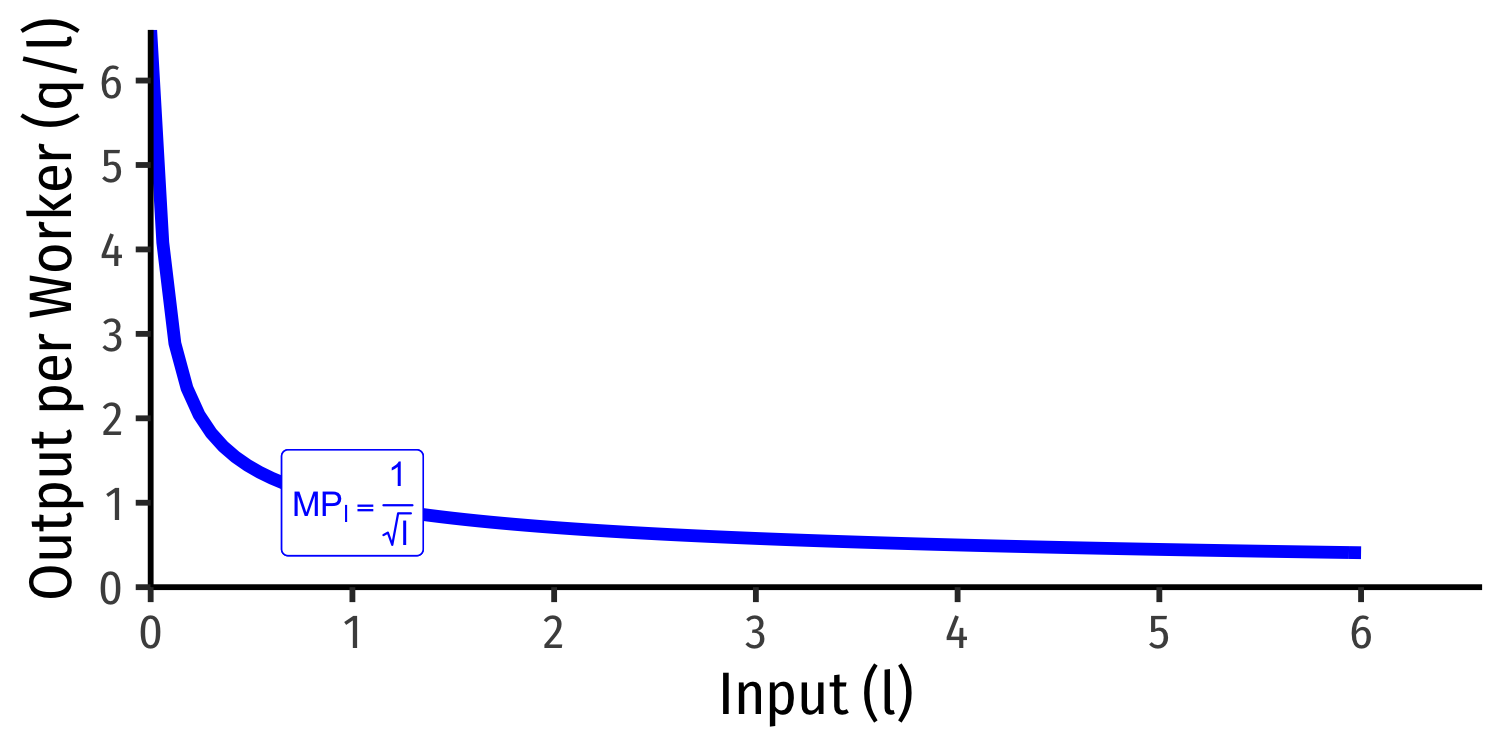
  • Marginal product of labor (MPl): additional output produced by adding one more unit of labor (holding k constant) MPl=ΔqΔl

  • MPl is the slope of TP at every value of l!

  • Note: via calculus: ∂q∂l

Marginal Product of Capital

  • Marginal product of capital (MPk): additional output produced by adding one more unit of capital (holding l constant) MPk=ΔqΔk

  • MPk is the slope of TP at every value of k!

  • Note: via calculus: ∂q∂k

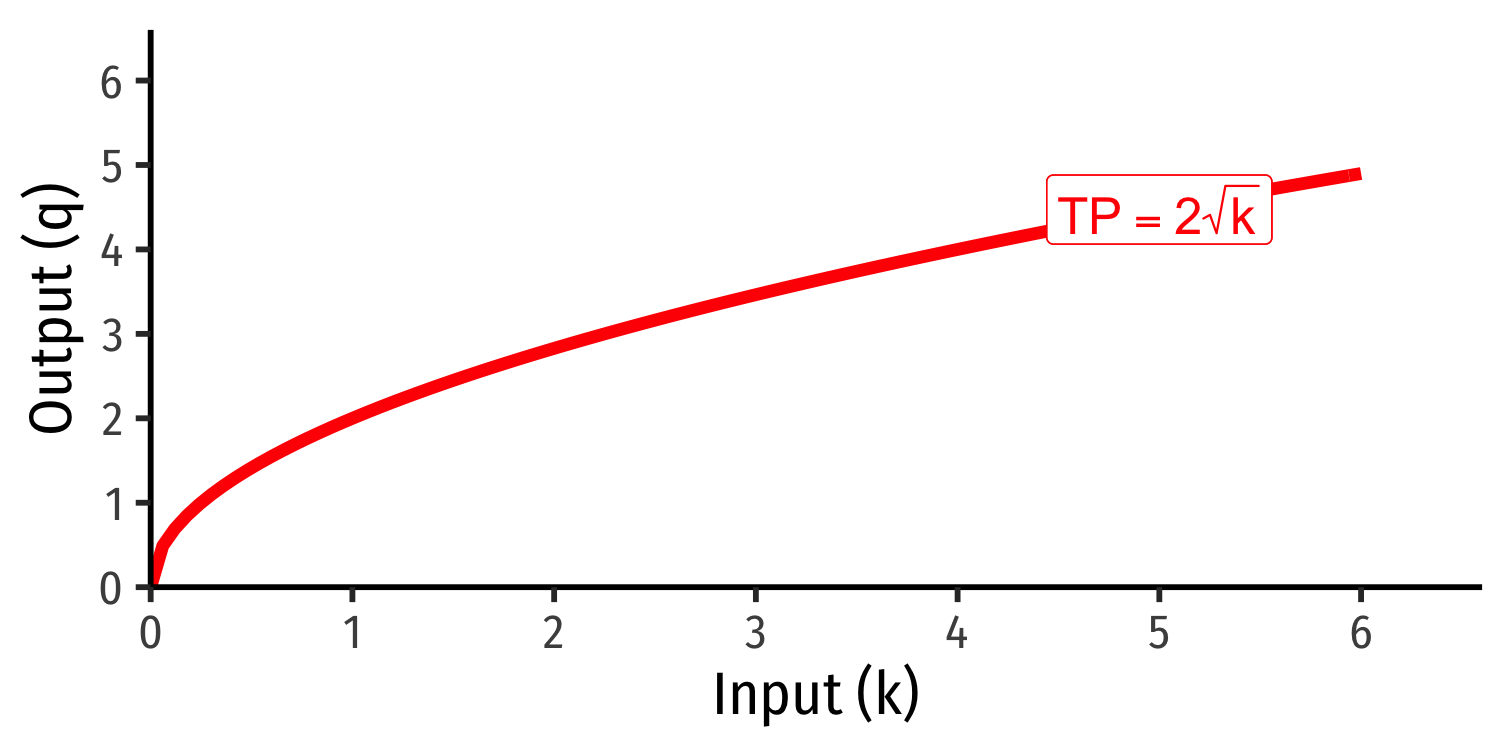
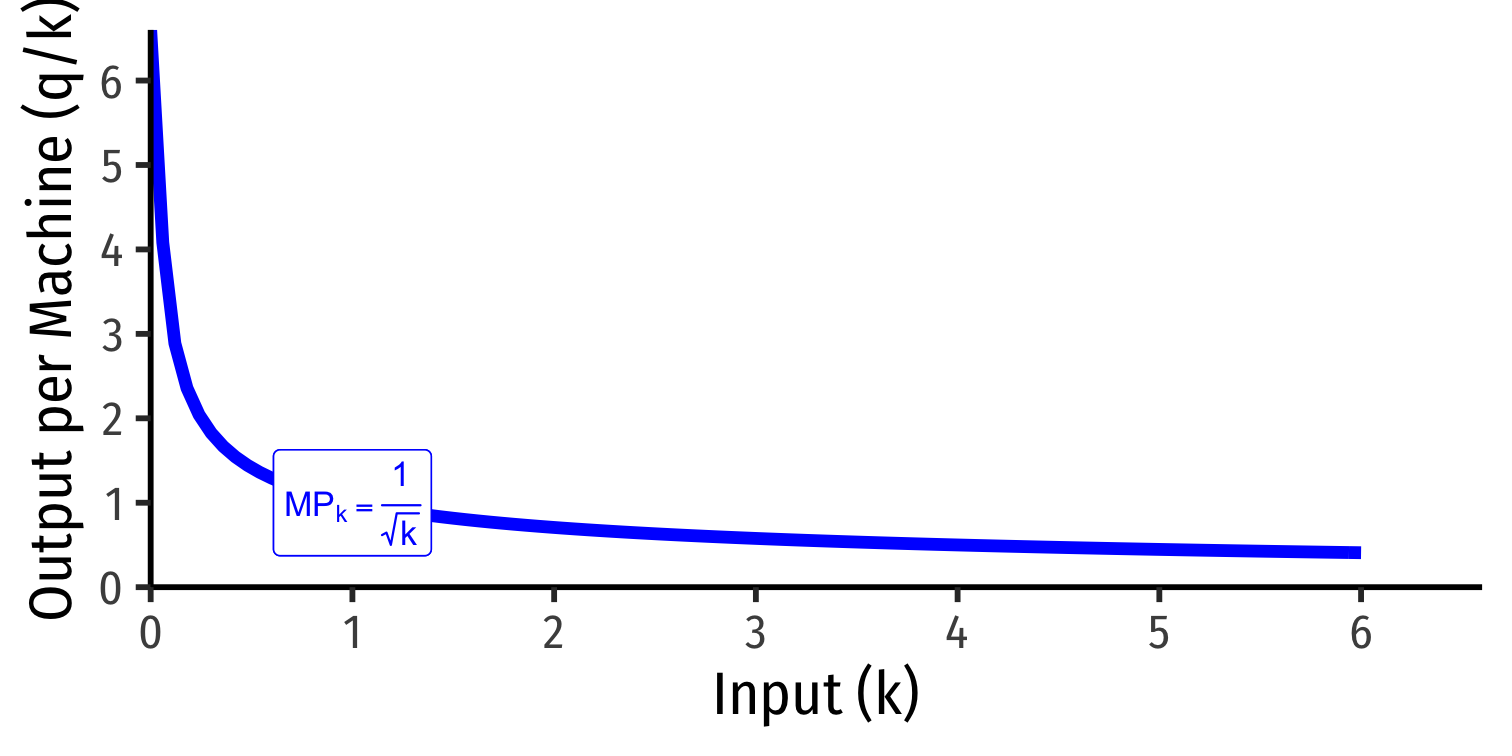
Diminishing Returns

  • Law of Diminishing Returns: adding more of one factor of production holding others constant will result in successively lower increases in output

  • In order to increase output, firm will need to increase all factors!

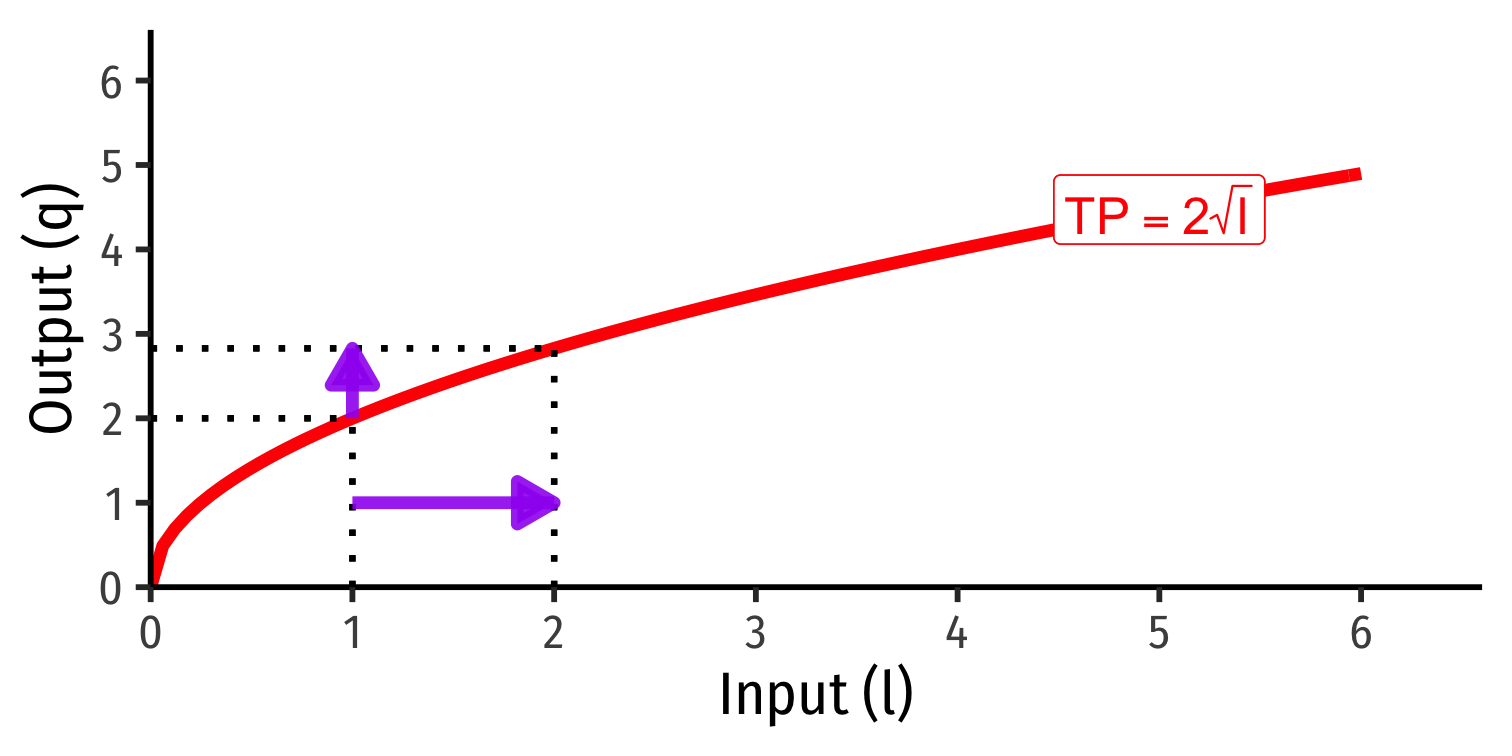
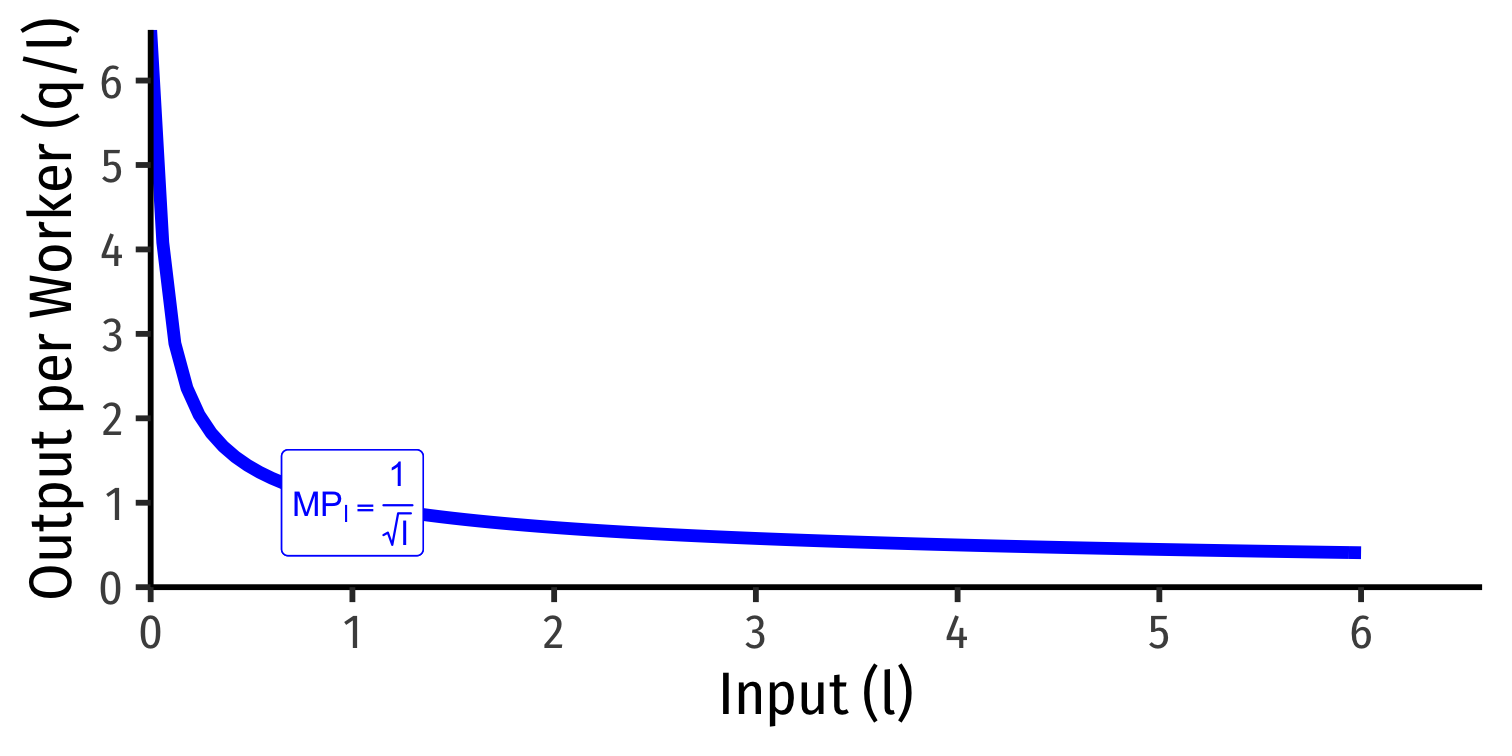
Diminishing Returns

  • Law of Diminishing Returns: adding more of one factor of production holding others constant will result in successively lower increases in output1

  • In order to increase output, firm will need to increase all factors!

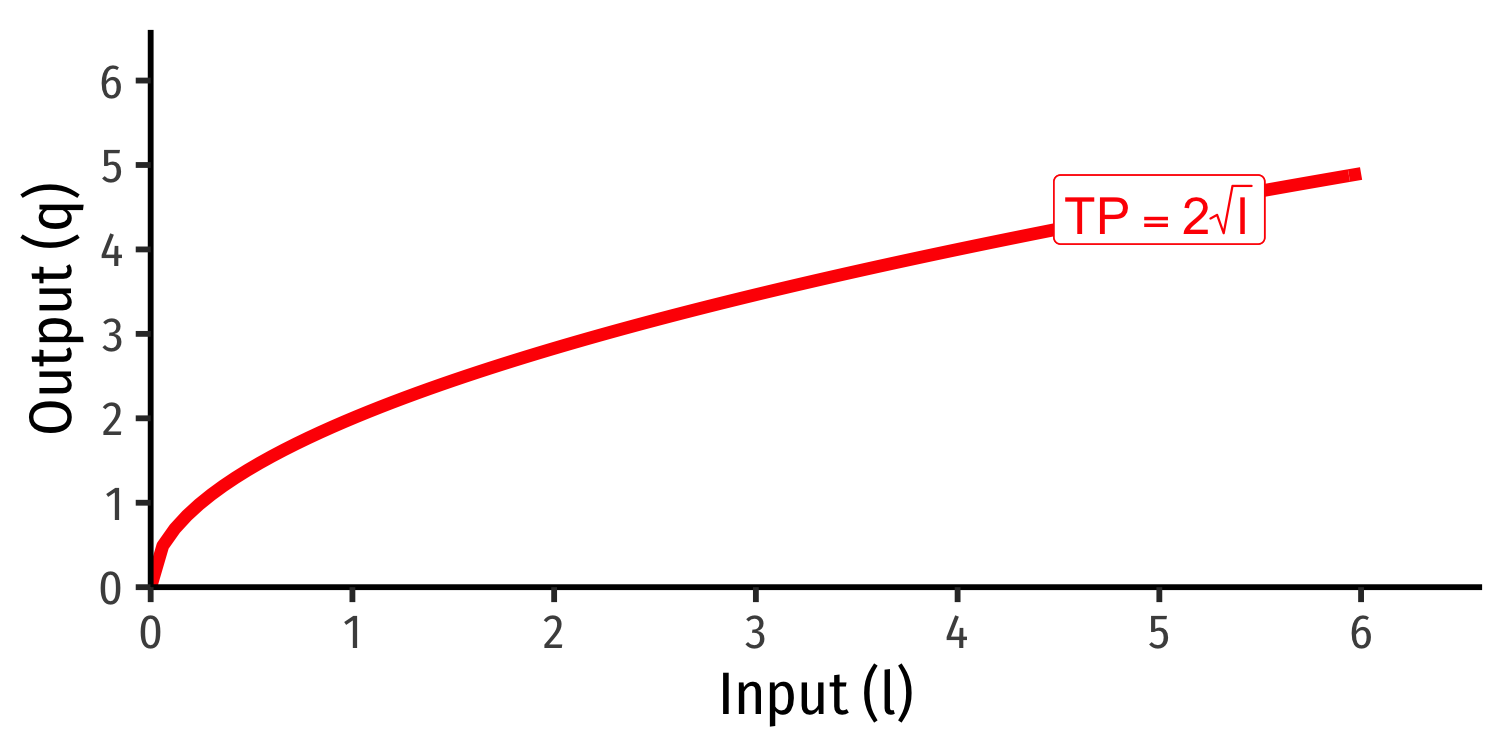
Average Product of Labor

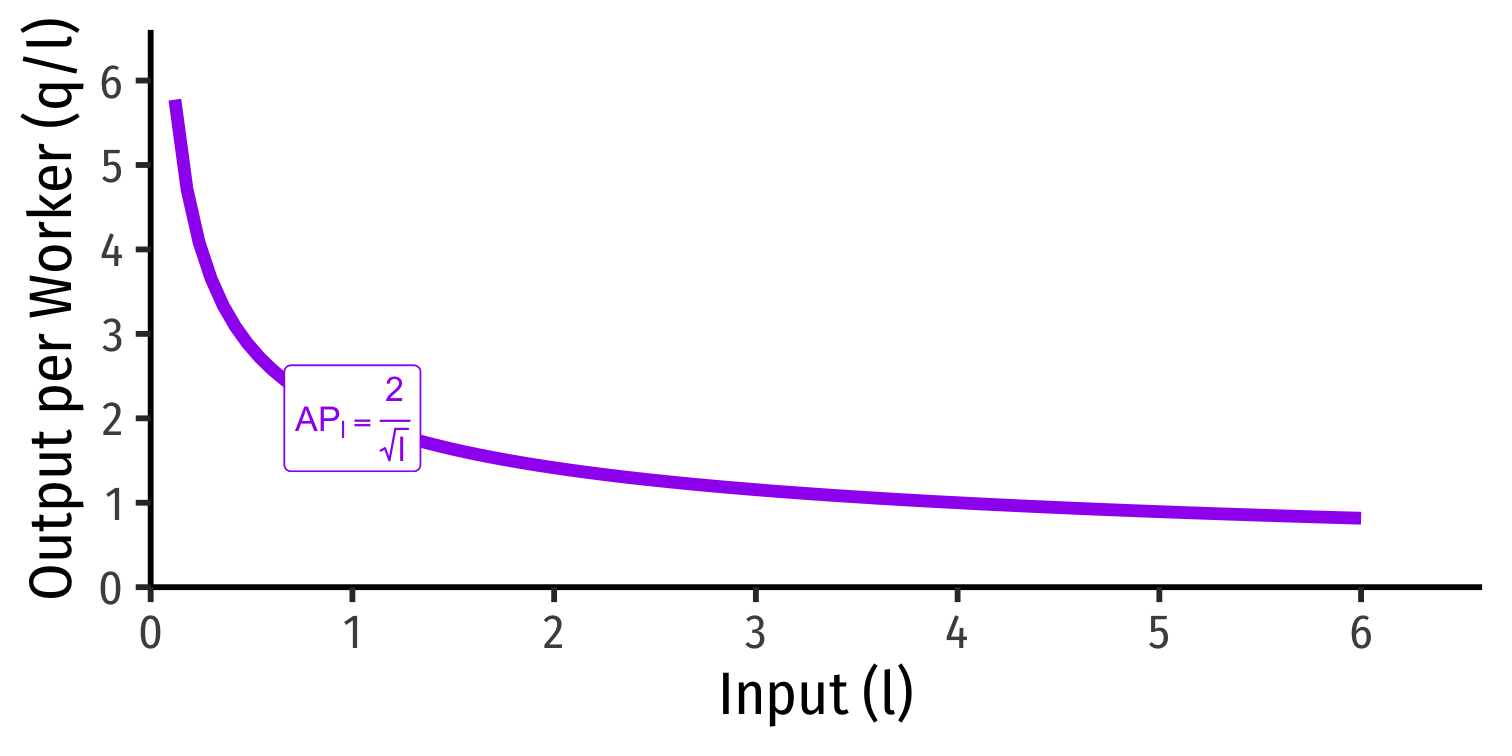
  • Average product of labor (APl): total output per worker APl=ql

  • A measure of labor productivity

  • Average product of capital (APk): total output per unit of capital APk=qk

The Long Run

  • In the long run, all factors of production are variable

q=f(k,l)

  • Can build more factories, open more storefronts, rent more space, invest in machines, etc.

  • So the firm can choose both l and k

The Firm's Problem

  • Based on what we've discussed, we can fill in a constrained optimization model for the firm

    • But don't write this one down just yet!

  • The firm's problem is:

  1. Choose: < inputs and output >

  2. In order to maximize: < profits >

  3. Subject to: < technology >

Costs in Economics are Opportunity Costs

  • Costs in economics are different from common conception of "cost"
    • Accounting cost: monetary cost
    • Economic cost: value of next best use of resources given up (opportunity cost)

Costs in Economics are Opportunity Costs

  • Costs in economics are different from common conception of "cost"

    • Accounting cost: monetary cost
    • Economic cost: value of next best use of resources given up

  • This leads to the difference between

    • Accounting profit: revenues minus accounting costs
    • Economic profit: revenues minues accounting & opportunity costs

Another Helpful Perspective

  • Another helpful perspective:
    • "Accounting cost": what you historically paid for a resource
    • "Economic cost: what you can currently get in the market for a resource
    • Its value in alternative uses (market price, measuring the opp cost)

The Accounting vs. Economic Point of View I

  • Helpful to consider two points of view:
    • "Accounting point of view": are you taking in more cash than you are spending?
    • "Economic point of view: is your product you making the best social use of your resources (i.e. are there higher-valued uses of your resources you are keeping them away from)?

The Accounting vs. Economic Point of View II

  • Social implications: are consumers best off with you using scarce resources (with alternative uses!) to produce your current product?

  • Remember: this is an economics course, not a business course!

    • What might be good/bad for one business might have bad/good consequences for society!

Opportunity Costs

  • Each choice incurs an opportunity cost

Examples:

  • If you choose to start a business, you may give up your salary at your current job
  • If you own your firm, your labor in it could be put towards working elsewhere
  • If you invest in a factory, you give up other investment opportunities
  • If you use an office building you own, you cannot rent it to other people
  • If you own land on which you farm, you cannot rent the land to others

Opportunity Cost is Hard for People

Opportunity Costs vs. Sunk Costs

  • Opportunity cost is a forward-looking concept

  • Choices made in the past with non-recoverable costs are called sunk costs

  • Sunk costs should not enter into future decisions

  • Many people have difficulty letting go of unchangeable past decisions: sunk cost fallacy

The Sunk Cost Fallacy

Common Sunk Costs in Business

  • Licensing fees, long-term lease contracts

  • Specific capital (with no alternative use): uniforms, menus, signs

  • Research & Development spending

  • Advertising spending

Costs in the Short Run

Costs in the Short Run

  • Total cost function, C(q) relates output q to the total cost of production C

C(q)=f+VC(q)

Costs in the Short Run

  • Total cost function, C(q) relates output q to the total cost of production C

C(q)=f+VC(q)

  • Two kinds of costs:

1. Fixed costs, f are costs that do not vary with output

  • Only true in the short run! (Consider this the cost of maintaining your capital)

Costs in the Short Run

  • Total cost function, C(q) relates output q to the total cost of production C

C(q)=f+VC(q)

  • Two kinds of costs:

1. Fixed costs, f are costs that do not vary with output

  • Only true in the short run! (Consider this the cost of maintaining your capital)

2. Variable costs, VC(q) are costs that vary with output (notice the variable in them!)

  • Typically, the more production of q, the higher the cost
  • e.g. firm is hiring additional labor

Fixed vs. Sunk costs

  • What is the difference between fixed and sunk costs?

  • Sunk costs are a type of fixed cost that are not avoidable or recoverable

  • Many fixed costs can be avoided or changed in the long run

  • Common fixed, but not sunk, costs:

    • rent for office space
    • durable equipment
    • operating permits (that are renewed)

  • When deciding to stay in business, fixed costs matter, sunk costs do not!

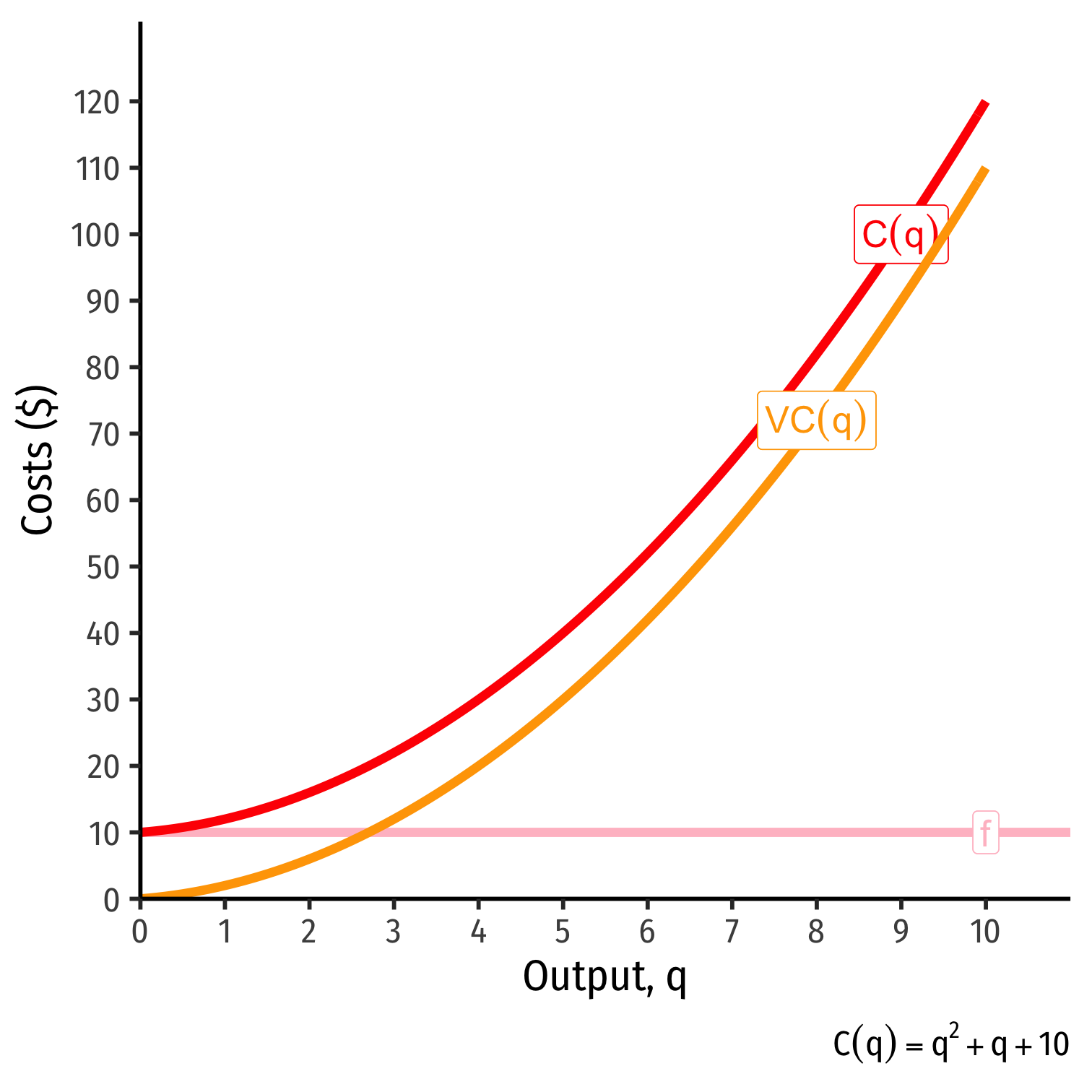
Cost Functions: Example

Example: Suppose your firm has the following total cost function:

C(q)=q2+q+10

  1. Write a function for the fixed costs, f.

  2. Write a function for the variable costs, VC(q).

Cost Functions: Example, Visualized

q f VC(q) C(q)
0 10 0 10
1 10 2 12
2 10 6 16
3 10 12 22
4 10 20 30
5 10 30 40
6 10 42 52
7 10 56 66
8 10 72 82
9 10 90 100
10 10 110 120

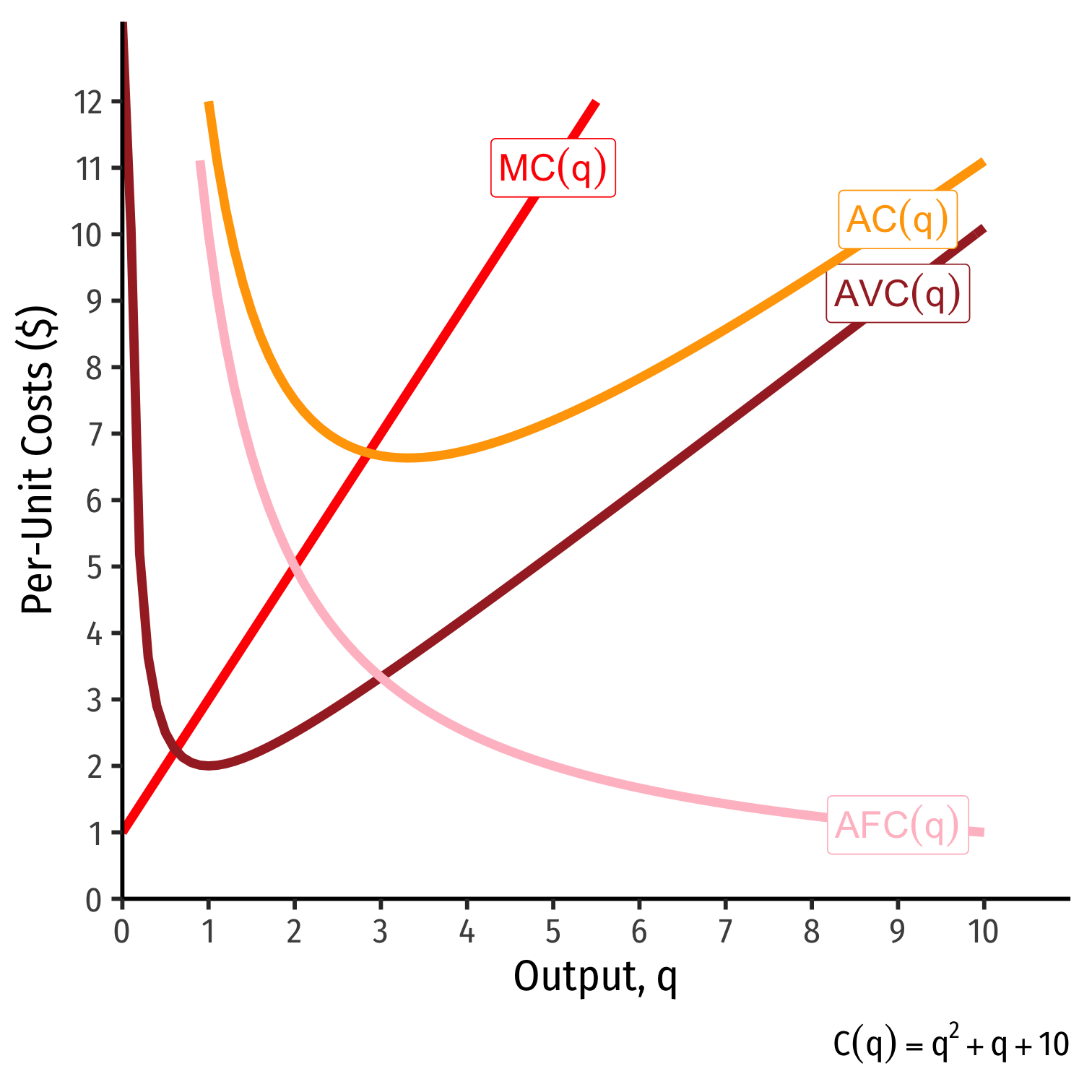
Average Costs

  • Average Fixed Cost: fixed cost per unit of output:

AFC(q)=fq

Average Costs

  • Average Fixed Cost: fixed cost per unit of output:

AFC(q)=fq

  • Average Variable Cost: variable cost per unit of output:

AVC(q)=VC(q)q

Average Costs

  • Average Fixed Cost: fixed cost per unit of output:

AFC(q)=fq

  • Average Variable Cost: variable cost per unit of output:

AVC(q)=VC(q)q

  • Average (Total) Cost: (total) cost per unit of output:

AC(q)=C(q)q

Marginal Cost

  • Marginal Cost is the change in cost for each additional unit of output produced:

MC(q)=ΔC(q)Δq

  • Calculus: first derivative of the cost function

  • Marginal cost is the primary cost that matters in making decisions

    • All other costs are driven by marginal costs
    • This is the main cost that firms can "see"

Average and Marginal Costs: Visualized

q C(q) MC(q) AFC(q) AVC(q) AC(q)
0 10 − − − −
1 12 2 10.00 2 12.00
2 16 4 5.00 3 8.00
3 22 6 3.33 4 7.30
4 30 8 2.50 5 7.50
5 40 10 2.00 6 8.00
6 52 12 1.67 7 8.70
7 66 14 1.43 8 9.40
8 82 16 1.25 9 10.25
9 100 18 1.11 10 11.10
10 120 20 1.00 11 12.00

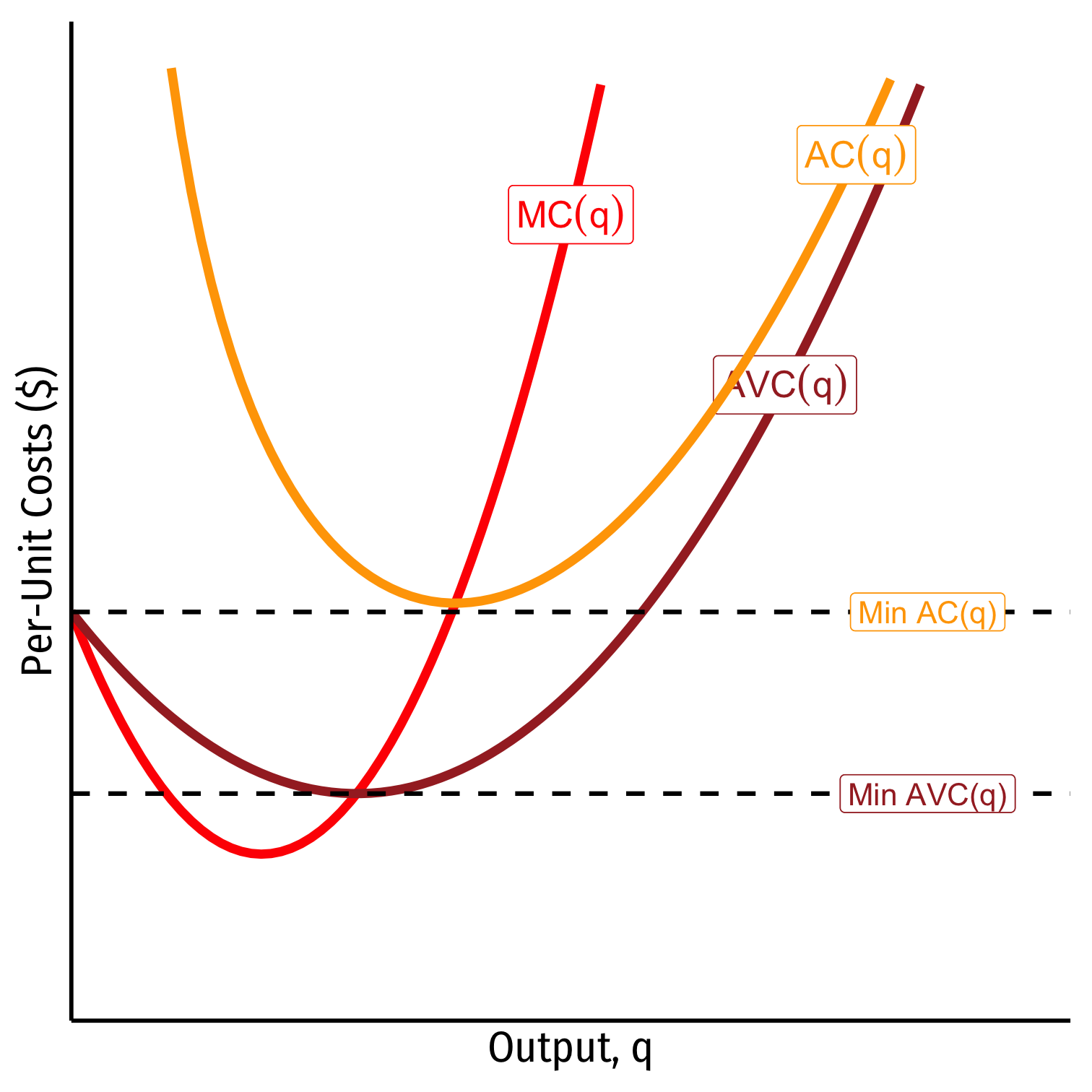
Relationship Between Marginal and Average

  • Relationship between a marginal and an average value:

  • Whenever marginal > average, average is increasing

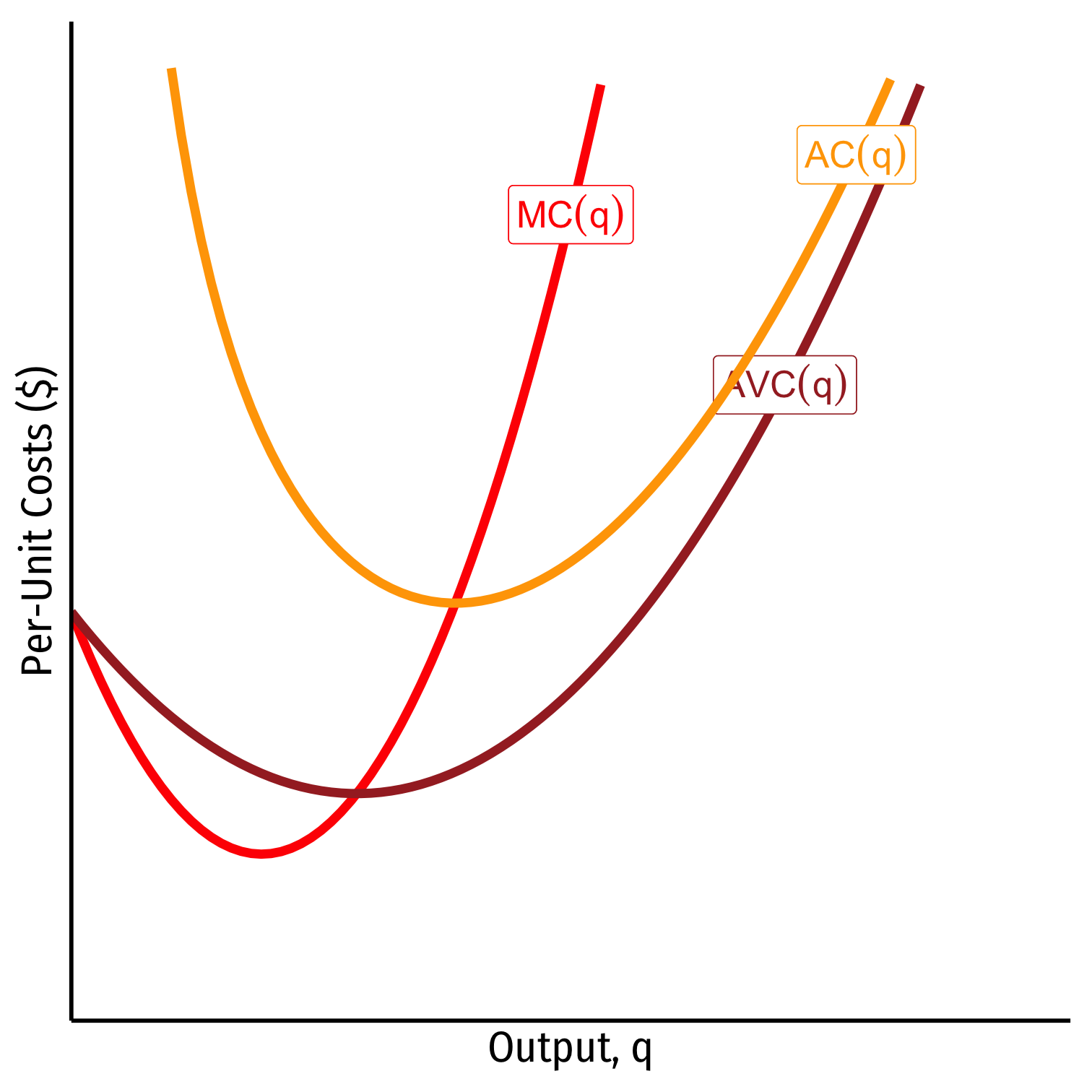
Relationship Between Marginal and Average

  • Relationship between a marginal and an average value:

  • Whenever marginal > average, average is increasing

  • Whenever marginal < average, average is decreasing

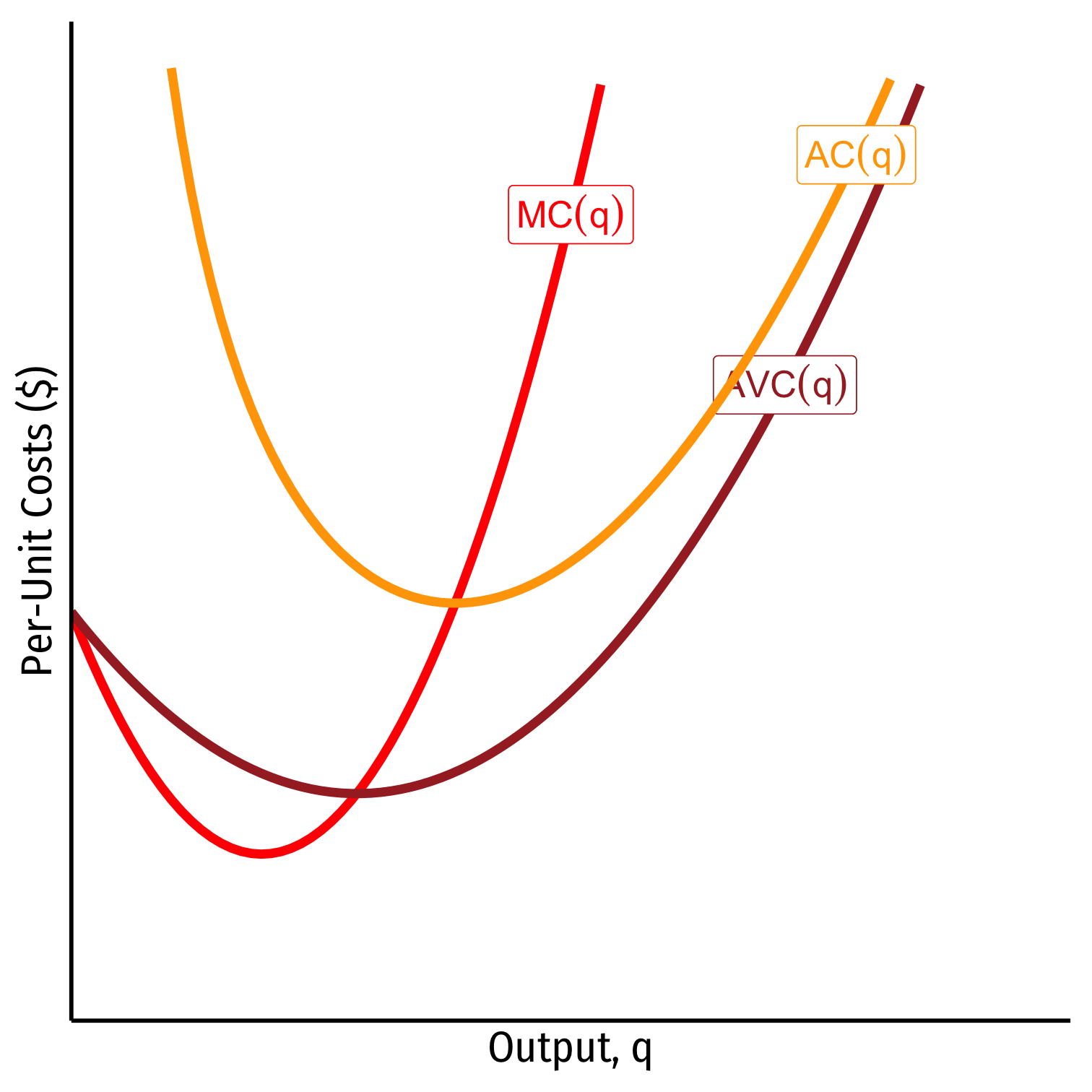
Relationship Between Marginal and Average

  • Relationship between a marginal and an average value:

  • Whenever marginal > average, average is increasing

  • Whenever marginal < average, average is decreasing

  • When marginal = average, average is maximized/minimized

  • When MC=AC, AC is at a minimum

  • When MC=AVC, AVC is at a minimum

  • Economic importance (later):

    • Break-even price and shut-down price

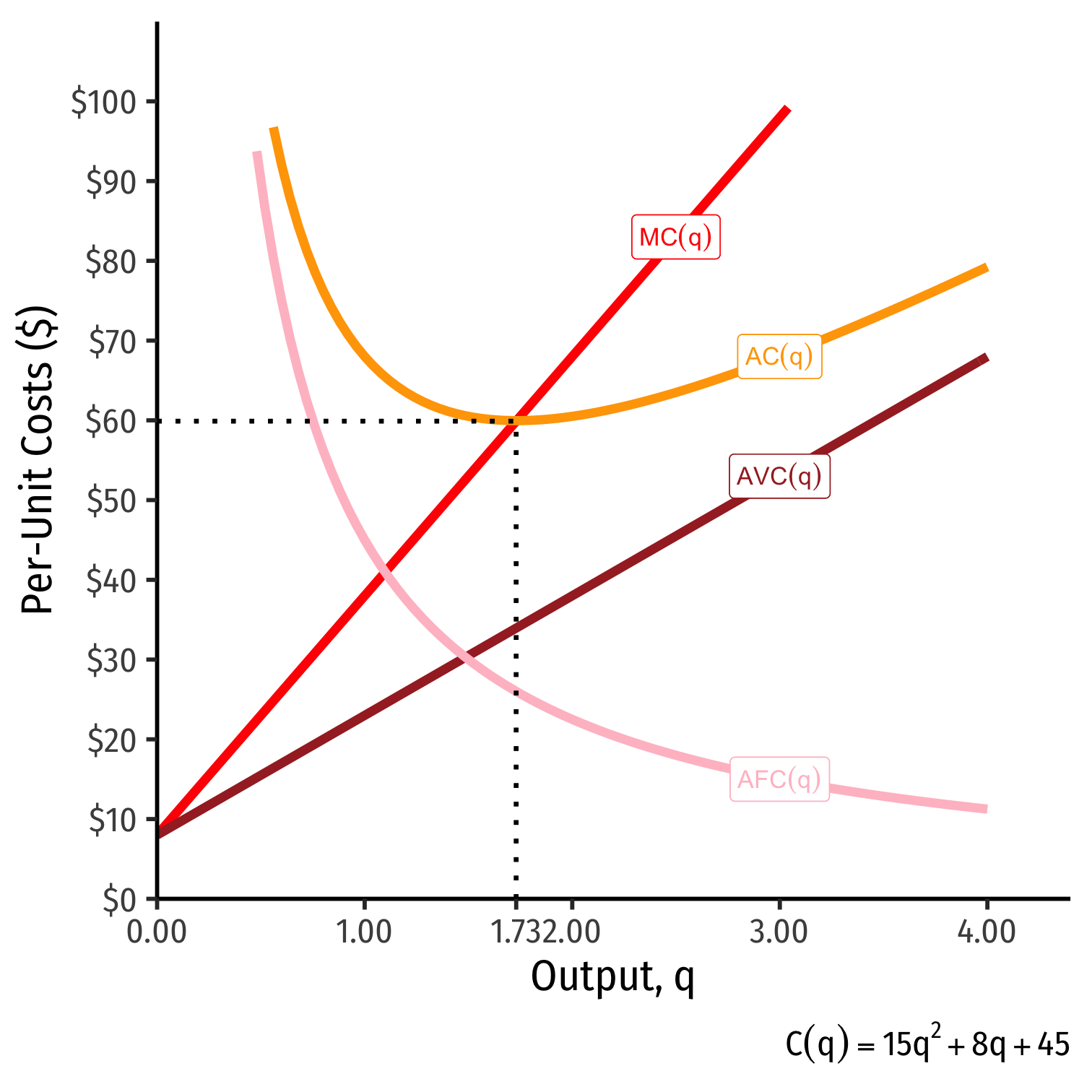
Costs: Example

Example: Suppose a firm's cost structure is described by: C(q)=15q2+8q+45MC(q)=30q+8

  1. Write expressions for the firm's fixed costs, variable costs, average fixed costs, average variable costs, and average (total) costs.

  2. Find the minimum average (total) cost.

  3. Find the minimum average variable cost.

Costs: Example: Visualized

Costs in the Long Run

Costs in the Long Run

  • In the long run, firm can change all factors of production, and vary the scale of production

  • Long run average cost, LRAC(q): cost per unit of output when the firm can change both l and k to make more q

  • Long run marginal cost, LRMC(q): change in long run total cost as the firm produce an additional unit of q (by changing both l and/or k)

Average Cost in the Long Run

  • In the long run, firm can choose k (factories, locations, etc)

  • Separate short run average cost (SRAC) curves for each amount of k potentially chosen

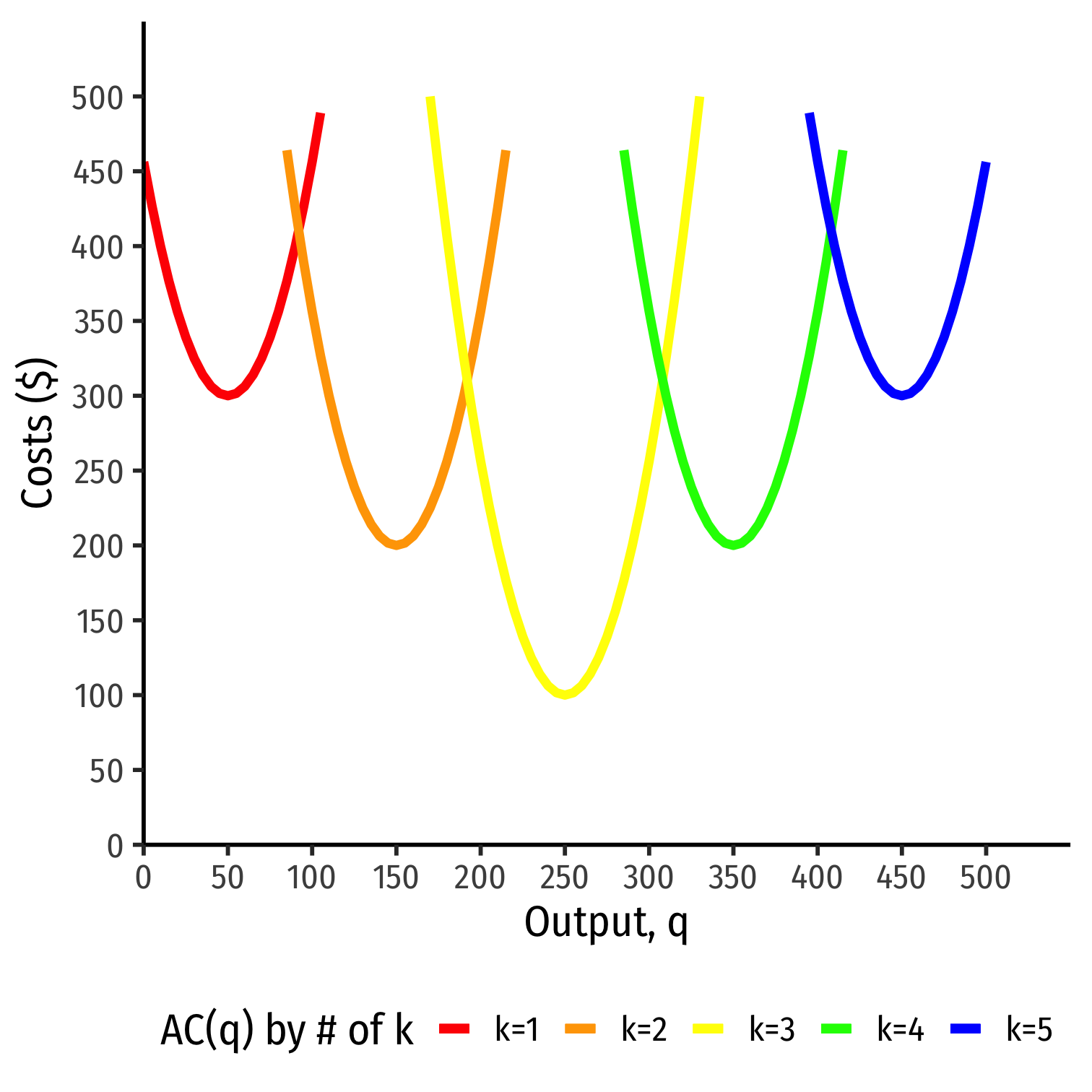
Average Cost in the Long Run

  • In the long run, firm can choose k (factories, locations, etc)

  • Separate short run average cost (SRAC) curves for each amount of k potentially chosen

  • Long run average cost (LRAC) curve "envelopes" the lowest (optimal) parts of all the SRAC curves!

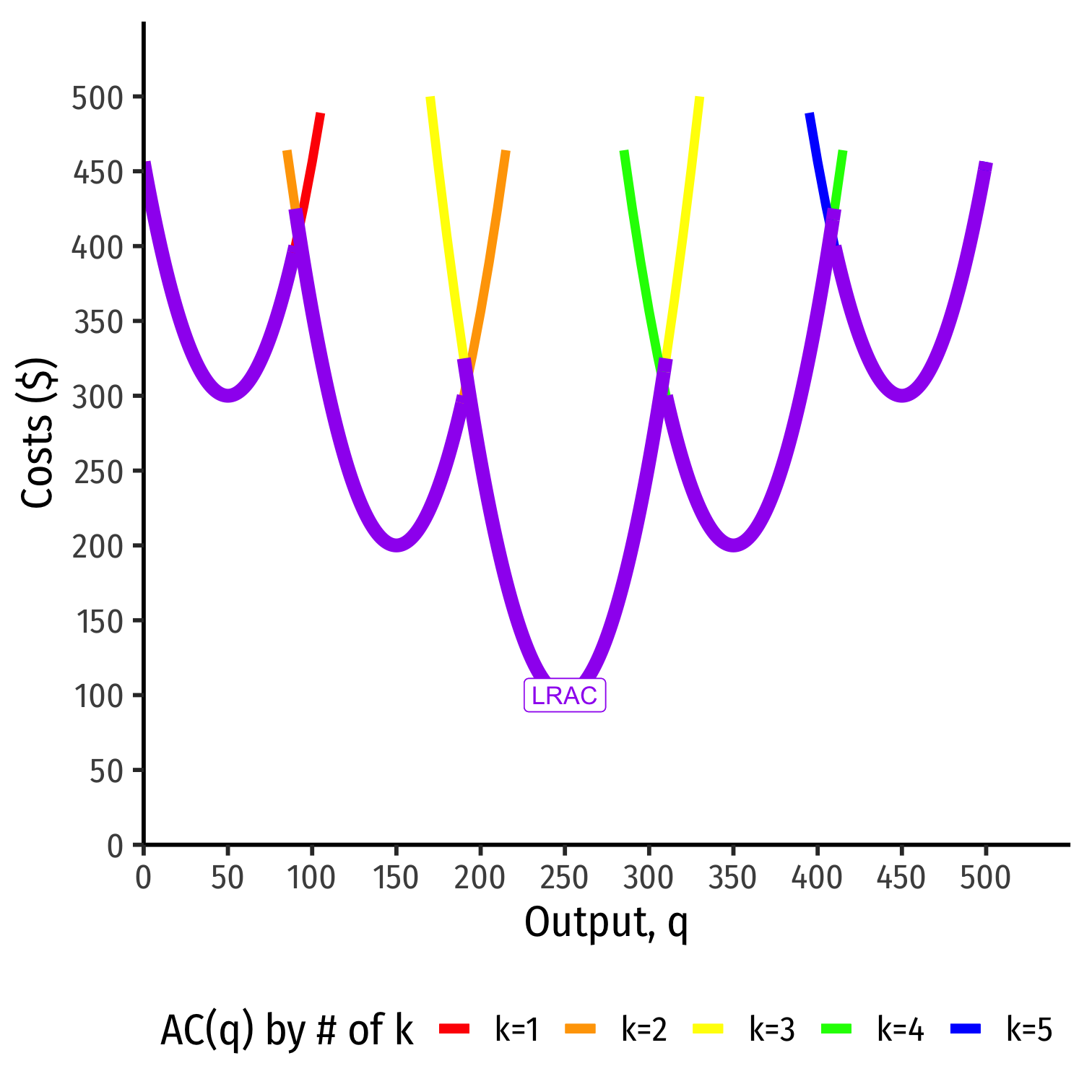
Long Run Costs & Scale Economies I

  • Further properties about costs based on scale economies of production:

  • Economies of scale: costs fall with output

  • Diseconomies of scale: costs rise with output

  • Constant economies of scale: costs don't change with output

  • Note economies of scale ≠ returns to scale!

    • RTS: a technological relationship between inputs & output
    • EOS: an economic relationship between output and average costs

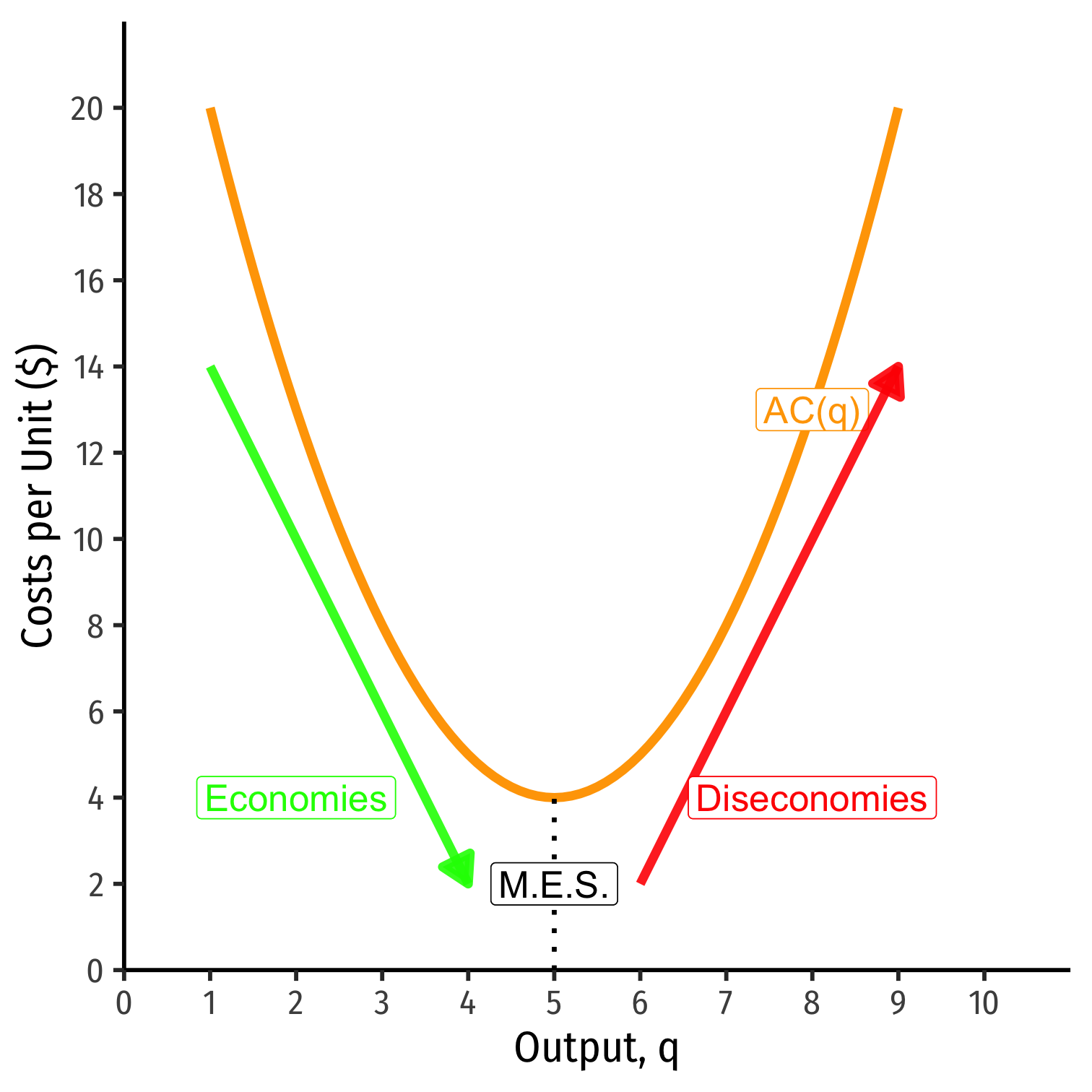
Long Run Costs & Scale Economies II

  • Minimum Efficient Scale: q with the lowest AC(q)

  • Economies of Scale: ↑q, ↓AC(q)

  • Diseconomies of Scale: ↑q, ↑AC(q)

Revenues

Revenues for Firms in Competitive Industries I

Revenues for Firms in Competitive Industries I

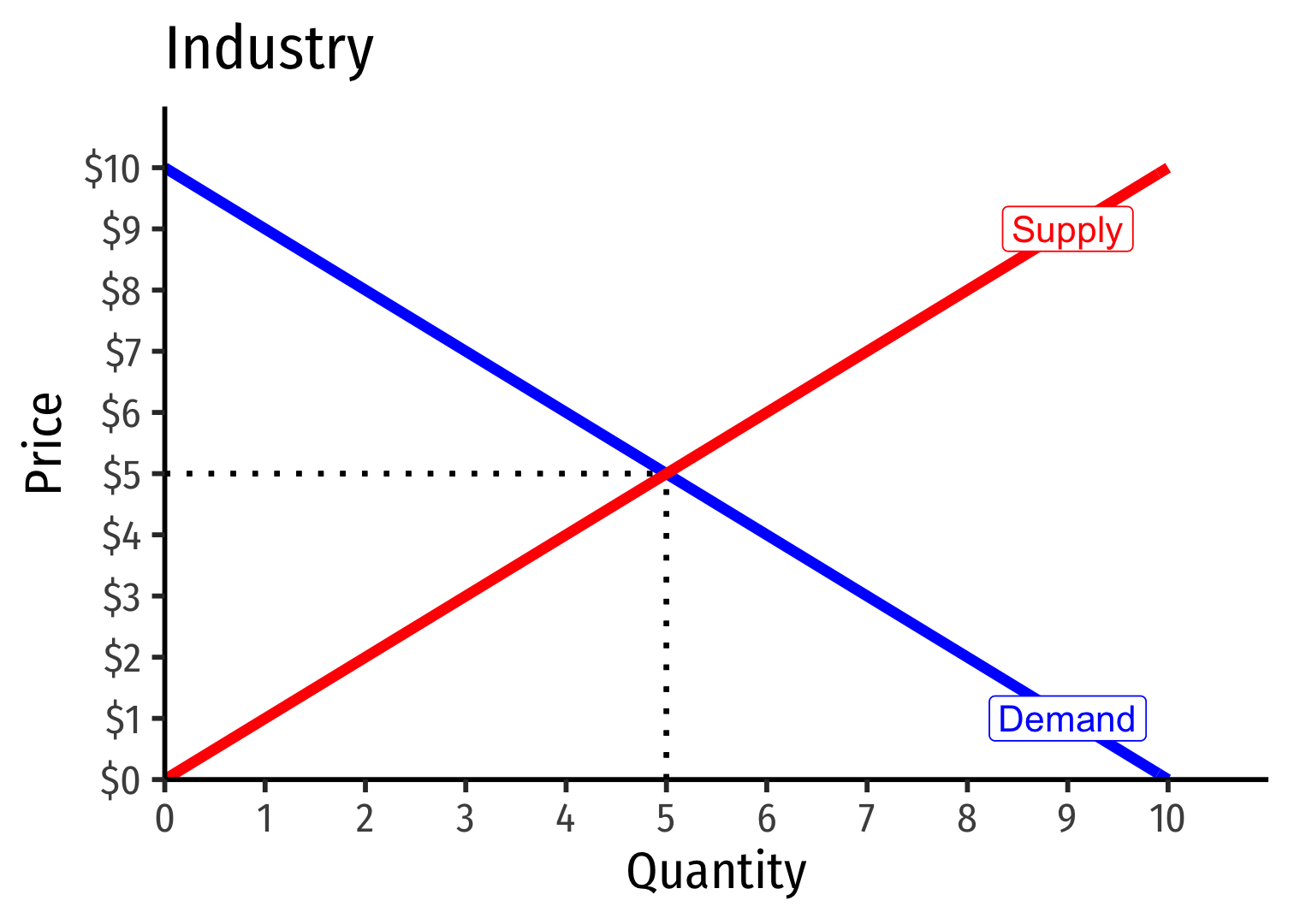
Revenues for Firms in Competitive Industries I

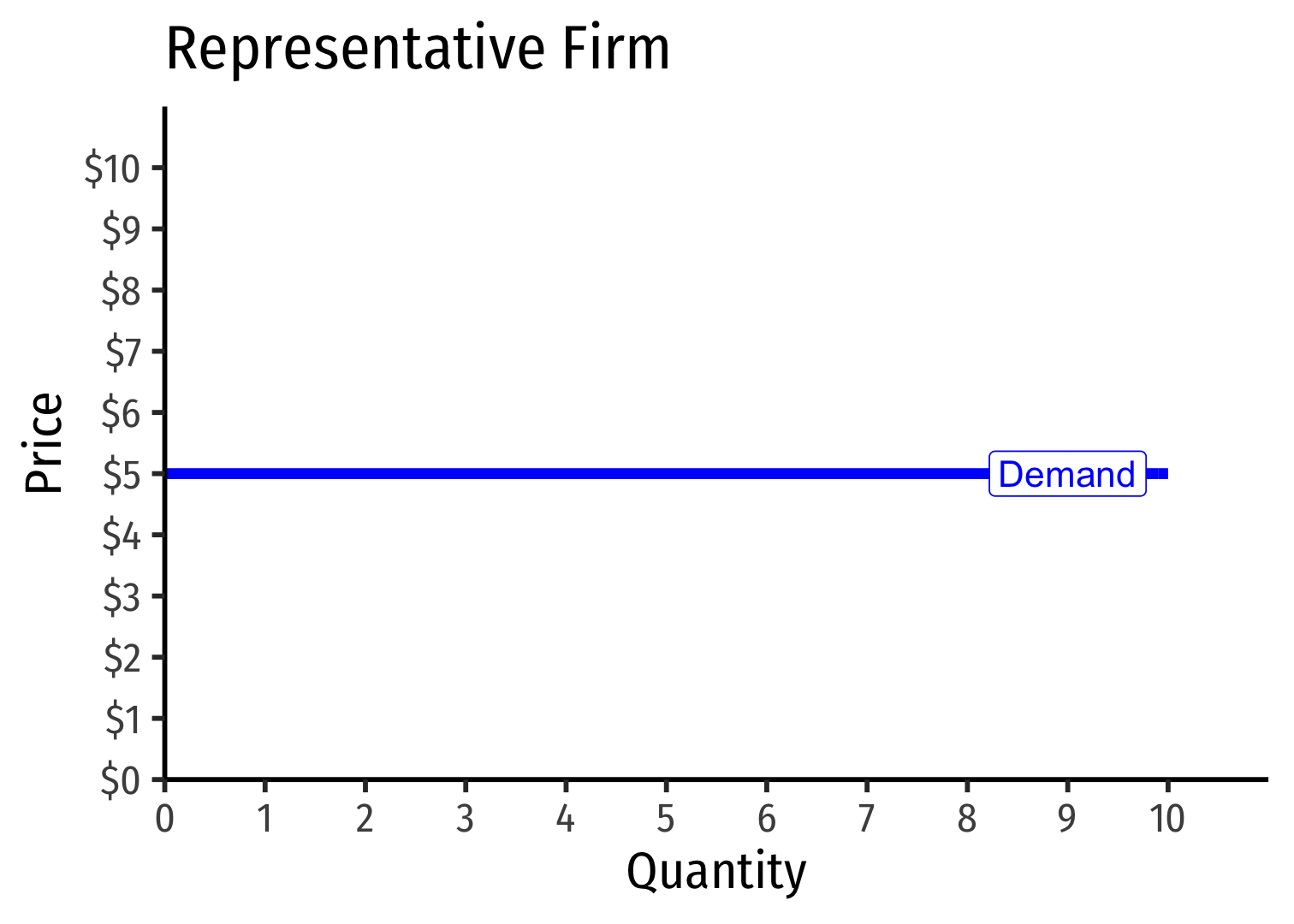
  • Demand for a firm's product is perfectly elastic at the market price

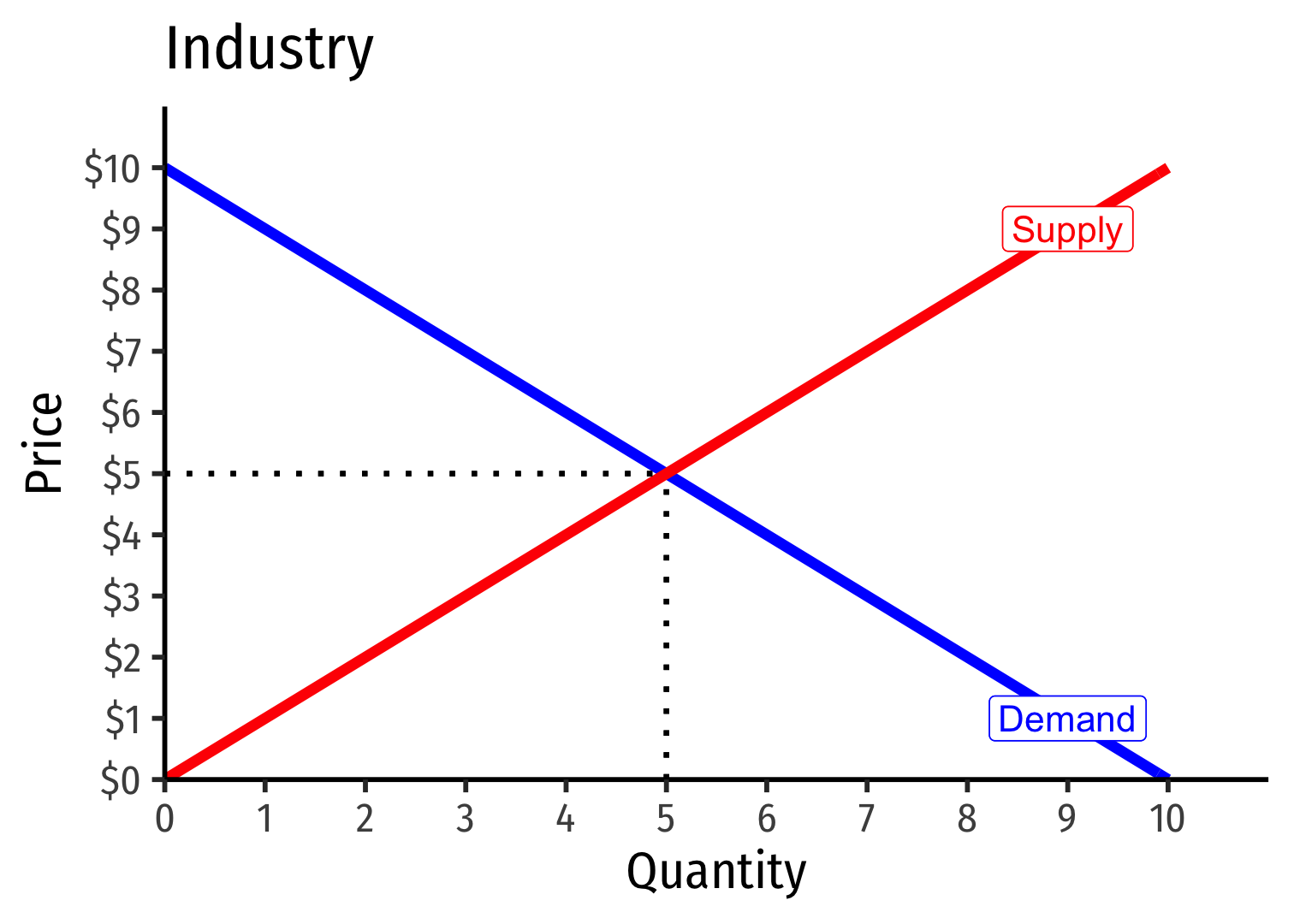
Revenues for Firms in Competitive Industries I

  • Demand for a firm's product is perfectly elastic at the market price

  • Where did the supply curve come from? You'll see

Revenues for Firms in Competitive Industries II

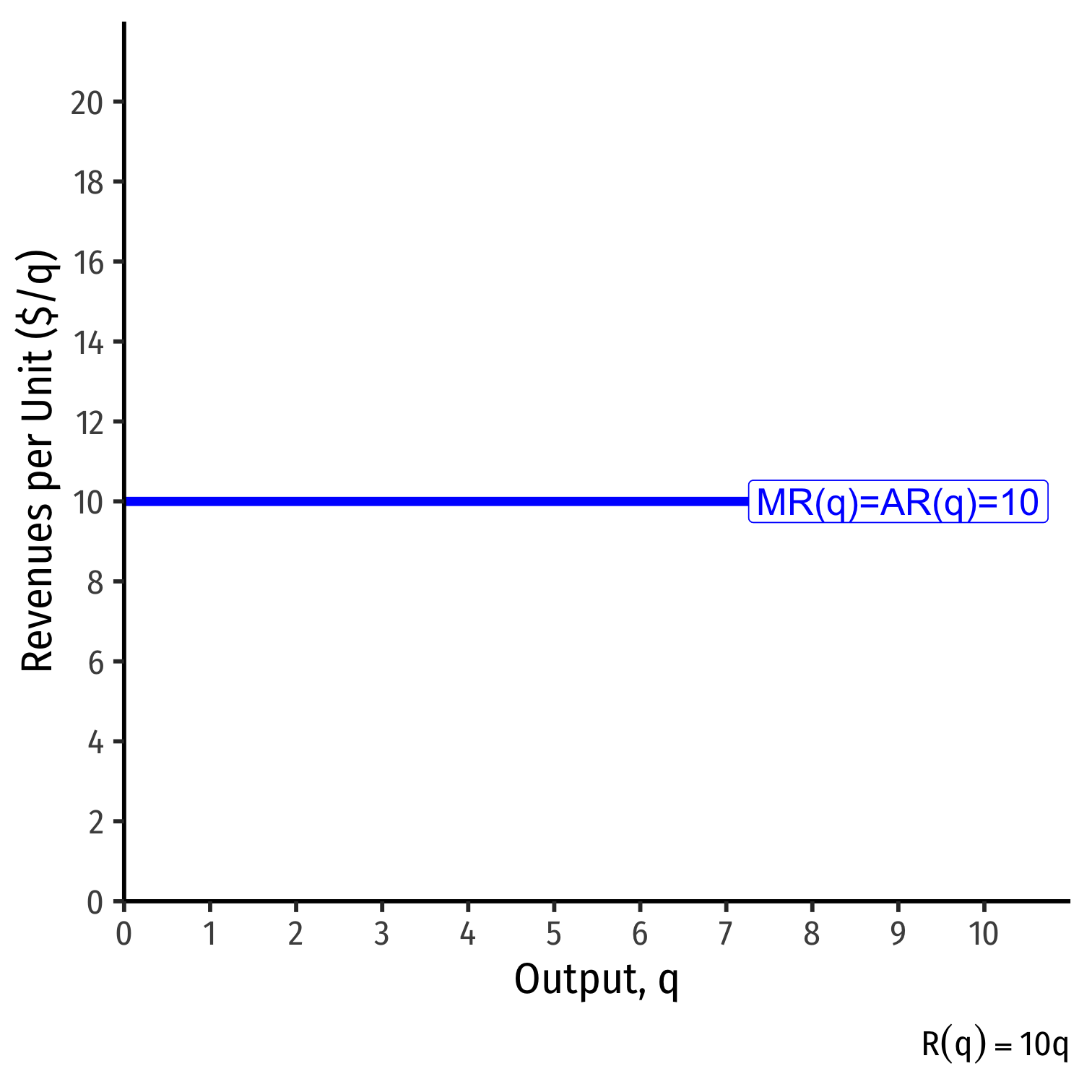
  • Total Revenue R(q)=pq

Average and Marginal Revenues

  • Average Revenue: revenue per unit of output AR(q)=Rq
    • Is always equal to the price! Why?

Average and Marginal Revenues

  • Average Revenue: revenue per unit of output AR(q)=Rq

    • Is always equal to the price! Why?

  • Marginal Revenue: change in revenues for each additional unit of output sold: MR(q)=ΔR(q)Δq≈R2−R1q2−q1

    • Calculus: first derivative of the revenues function
    • For a competitive firm, always equal to the price!

Average and Marginal Revenues: Example

Example: A firm sells bushels of wheat in a very competitive market. The current market price is $10/bushel.

Average and Marginal Revenues: Example

Example: A firm sells bushels of wheat in a very competitive market. The current market price is $10/bushel.

For the 1st bushel sold:

  • What is the total revenue?

  • What is the average revenue?

Average and Marginal Revenues: Example

Example: A firm sells bushels of wheat in a very competitive market. The current market price is $10/bushel.

For the 1st bushel sold:

  • What is the total revenue?

  • What is the average revenue?

For the 2nd bushel sold:

  • What is the total revenue?

  • What is the average revenue?

  • What is the marginal revenue?

Total Revenue, Example: Visualized

q R(q)
0 0
1 10
2 20
3 30
4 40
5 50
6 60
7 70
8 80
9 90
10 100

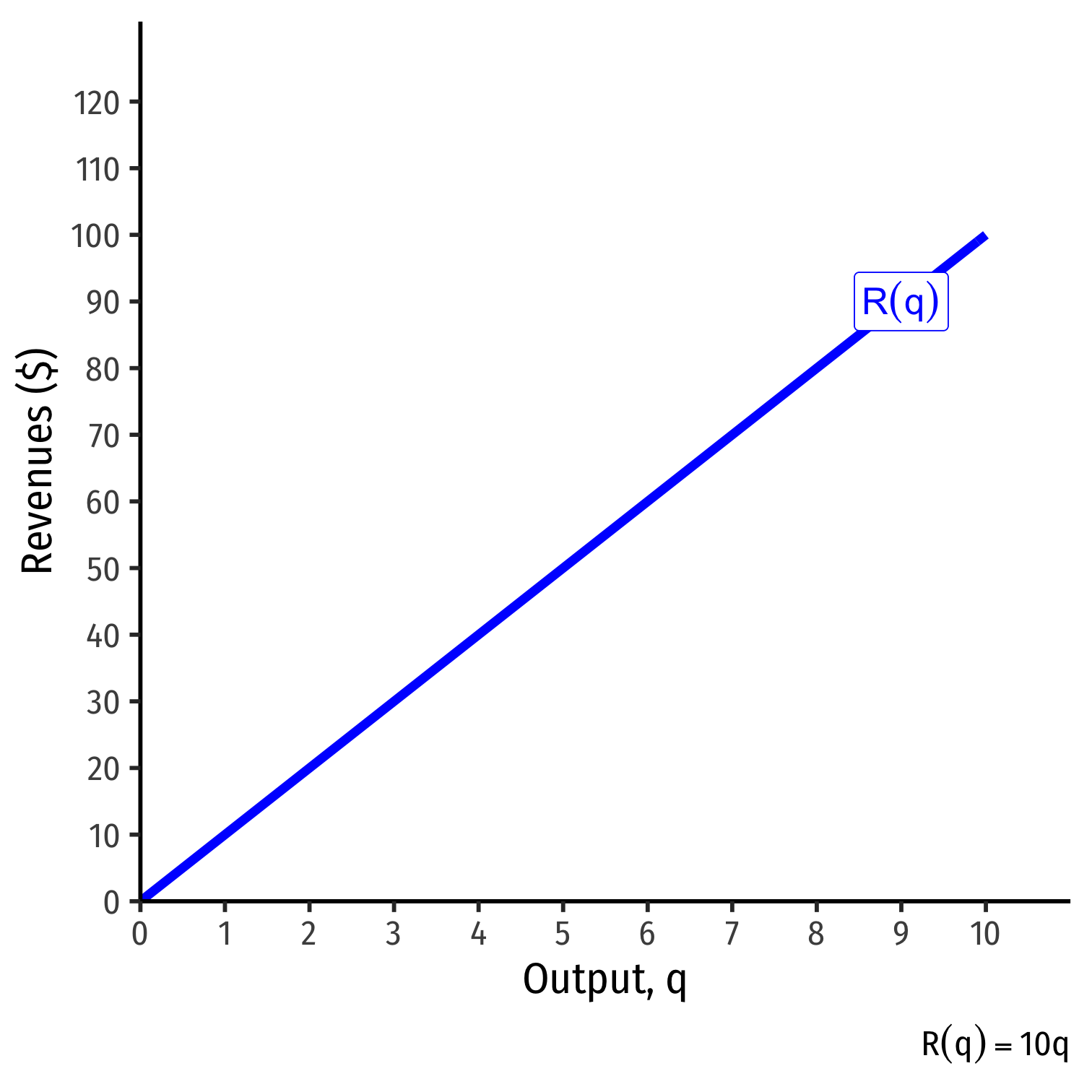
Average and Marginal Revenue, Example: Visualized

q R(q) AR(q) MR(q)
0 0 − −
1 10 10 10
2 20 10 10
3 30 10 10
4 40 10 10
5 50 10 10
6 60 10 10
7 70 10 10
8 80 10 10
9 90 10 10
10 100 10 10

Models Refresher

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow